В предыдущих лекциях обсуждалось правило кратчайшего пути и два алгоритма (или, возможно, системы) для поиска путей без петель через сеть. Существует широкий спектр таких систем—их слишком много, чтобы охватить их в отведенное время для изучения, - но для сетевых администраторв важно быть знакомыми хотя бы с некоторыми из этих систем. В этих лекциях сначала рассматривается алгоритм поиска кратчайшего пути Дейкстры, вектор пути и два различных алгоритма непересекающихся путей: Suurballe и Maximally Redundant Trees (MRTs). Наконец, в этих лекциях будет рассмотрена еще одна проблема, которую должны решить управляющие плоскости: обеспечение двусторонней связи через сеть.

Алгоритм Дейкстра: Пути одноадресной передачи без петель
Алгоритм Дейкстры Shortest Path First.
Алгоритм Дейкстры Shortest Path First (SPF), возможно, является наиболее широко известной и понятной системой для обнаружения Loop-Free путей в сети. Он используется двумя широко распространенными протоколами маршрутизации и во многих других повседневных системах, таких как программное обеспечение, предназначенное для поиска кратчайшего пути через дорожную сеть или для обнаружения соединений и паттернов соединений в социальных сетях.
Алгоритм Дейкстры в псевдокоде использует две структуры данных. Первый - это предварительный список или TENT; этот список содержит набор узлов, рассматриваемых для включения в дерево кратчайшего пути (Shortest Path Tree). Второй - PATH; этот список содержит набор узлов (а следовательно, и каналы), которые находятся в дереве кратчайшего пути.
01 move "me" to the TENT
02 while TENT is not empty {
03 sort TENT
04 selected == first node on TENT
05 if selected is in PATH {
06 *do nothing*
07 }
08 else {
09 add selected to PATH
10 for each node connected to selected in TOPO
11 v = find node in TENT
12 if (!v)
13 move node to TENT
14 else if node.cost < v.cost
15 replace v with node on TENT
16 else
17 remove node from TOPO
18 }
19 }
Как всегда, алгоритм менее сложен, чем кажется на первый взгляд; ключом является сортировка двух списков и порядок, в котором узлы обрабатываются вне списка TENT. Вот несколько примечаний к псевдокоду перед рассмотрением примера:
- Процесс начинается с копии базы данных топологии, называемой здесь TOPO; это будет яснее в примере, но это просто структура, содержащая исходные узлы, целевые узлы и стоимость связи между ними.
- TENT - это список узлов, которые можно условно считать кратчайшим путем к любому конкретному узлу.
- PATH - это дерево кратчайшего пути (SPT), структура, содержащая loop-free путь к каждому узлу и следующий переход от «меня» к этому узлу.
- Первым важным моментом в этом алгоритме является сохранение только узлов, уже каким-то образом связанных с узлом в списке PATH в TENT; это означает, что кратчайший путь в TENT - это следующий кратчайший путь в сети.
- Второй важный момент в этом алгоритме - это сравнение между любыми существующими узлами TENT, которые подключаются к одному и тому же узлу; это, в сочетании с сортировкой TENT и отделением TENT от PATH, выполняет правило кратчайшего пути.
Имея в виду эти моменты, рисунки с 1 по 9 используются для иллюстрации работы алгоритма SPF Дейкстры.

На каждой из следующих иллюстраций вместе с сопроводительным описанием показан один шаг алгоритма SPF в этой сети, начиная с рисунка 2.
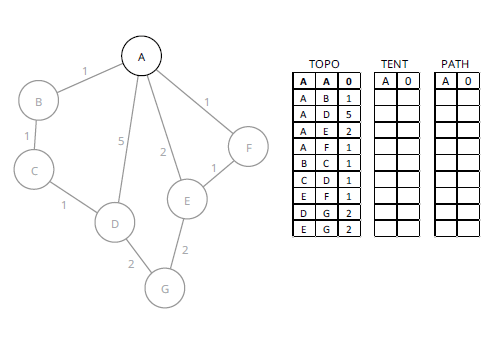
В точке, показанной на рисунке 2, A был перемещен из TOPO в TENT, а затем в PATH. Стоимость исходного узла всегда равна 0; эта линия включена для начала расчета SPF. Это представляет строки с 01 по 09 в псевдокоде, показанном ранее. На рисунке 3 показан второй этап расчета SPF.
На рисунке 3 каждый узел, подключенный к A, был перемещен из TOPO в TENT; это строки с 10 по 17 в псевдокоде, показанном ранее. Когда этот шаг начался, в TENT была только A, поэтому в TENT нет существующих узлов, которые могли бы вызвать какие-либо сравнения метрик. Теперь TENT отсортирован, и выполнение продолжается со строки 03 в псевдокоде. Рисунок 4 демонстрирует это.
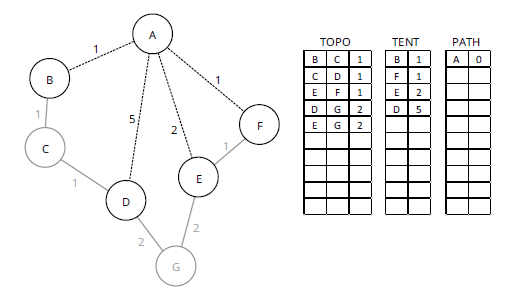
На рисунке 4 один из двух путей с кратчайшей стоимостью - к B и F, каждый со стоимостью 1 - был выбран и перемещен в PATH (строки 05–09 в псевдокоде, показанном ранее). Когда B перемещается из TENT в PATH, любые узлы с началом B в TOPO перемещаются в TENT (строки 10-17 в псевдокоде). Обратите внимание, что C еще не был в TENT, прежде чем он был задействован посредством перехода B к PATH, поэтому сравнение показателей не выполняется. Стоимость для C - это сумма стоимости его предшественника в PATH (который равен B со стоимостью 1) и связи между двумя узлами; следовательно, C добавляется к TENT со стоимостью 2. TENT сортируется (строка 3 псевдокода), поэтому процесс готов к повторному запуску. На рисунке 5 показан следующий шаг в этом процессе.
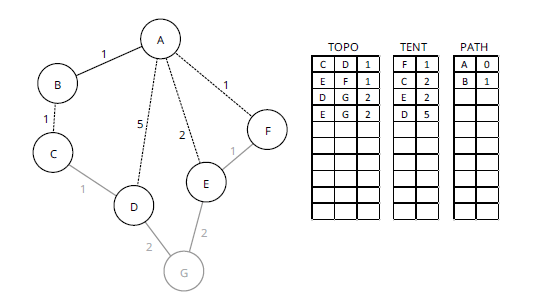
На рисунке 5 был выбран кратчайший путь к TENT, и F переместился от TENT к PATH. Между F и E существует связь (показанная на предыдущих иллюстрациях как [E, F]), но путь через F к E имеет ту же стоимость, что и путь [A, E], поэтому эта линия не добавляется в TENT. Скорее он остается неактивным, поскольку не рассматривается для включения в SPT, и удаляется из TOPO. На рисунке 6 показан следующий шаг в процессе, который переместит один из путей метрики 2 в PATH.
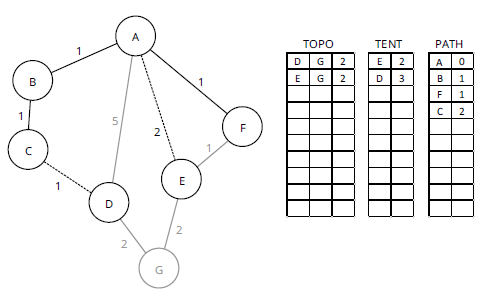
Примечание. Большинство реальных реализаций поддерживают перенос нескольких путей с одинаковой стоимостью из TENT в PATH, поэтому они могут пересылать трафик по всем каналам с одинаковой метрикой. Это называется многолучевым распространением с равной стоимостью или ECMP. Для этого есть несколько различных способов, но они в этих лекциях не рассматриваются.
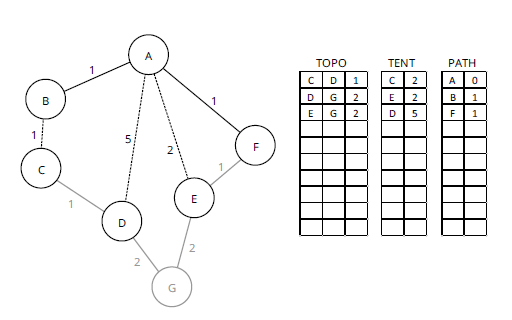
На рисунке 6 путь к C через B со стоимостью 2 был перемещен в PATH, а путь к D через [A, B, C, D] перемещен в TENT. Однако при перемещении этого пути к TENT строка 11 в псевдокоде находит существующий путь к D в TENT, путь [A, D], со стоимостью 5. Метрика нового пути, 3, ниже чем метрика существующего пути, 5, поэтому путь [A, D] удаляется из TENT, когда добавляется путь [A, B, C, D] (строка 15 в псевдокоде). На рисунке 7 показан следующий шаг, на котором линия оставшейся стоимости 2 перемещается из TENT в PATH.
На рисунке 7 путь к E стоимостью 2 был перемещен из TENT в PATH. G был перемещен в TENT стоимостью 4 (сумма [A, E] и [E, G]). Другой сосед E, F, исследуется, но он уже находится в PATH, поэтому не рассматривается для включения в TENT. На рисунке 8 показан следующий шаг, который перемещает D в PATH.
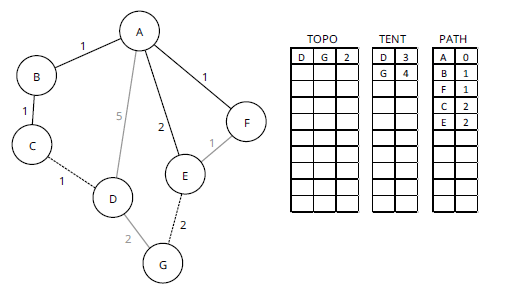
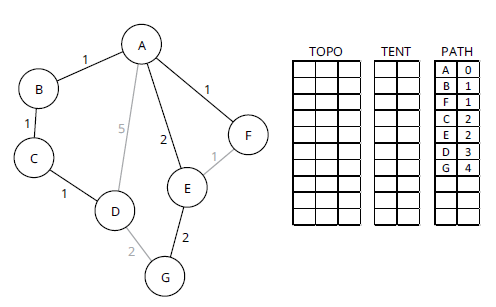
На рисунке 8 D общей стоимостью 3 перемещен из TENT в PATH. Это учитывает соседа D, G, последнюю запись в TOPO, для TENT. Однако уже существует путь к G с общей стоимостью 4 через [A, E, G], поэтому строка 14 в псевдокоде завершается ошибкой, и путь [D, G] удаляется из TOPO. Это последний SPT.
Основная трудность в понимании алгоритма Дейкстры заключается в том, что правило кратчайшего пути не выполняется в одном месте (или на одном маршрутизаторе), как это происходит с Bellman-Ford или Diffusing Update Algorithm (DUAL). Кратчайший путь (по-видимому) проверяется только при перемещении узлов из TOPO в TENT - но на самом деле сортировка самого TENT выполняет другую часть правила кратчайшего пути, и проверка по PATH для существующих узлов составляет еще один шаг в процесс, делающий процесс трехступенчатым:
- Если путь к узлу длиннее, чем любой из TENT, то путь к TENT является более коротким путем по всей сети.
- Путь, который поднялся к вершине TENT через сортировку, является самым коротким к этому узлу в сети.
- Если путь перемещается к PATH от вершины TENT, это кратчайший путь к этому узлу в сети, и любые другие записи в TOPO к этому узлу следует отбросить.
При наличии базового алгоритма полезно рассмотреть некоторые оптимизации и расчет Loop-Free Alternates (LFAs) и remote Loop-Free Alternates (rLFAs).
Частичный и инкрементный SPF
Нет особой причины, по которой весь SPT должен перестраиваться каждый раз, когда происходит изменение топологии сети или информации о доступности. Рассмотрим рисунок 9 для объяснения.
Предположим, G теряет связь с 2001: db8: 3e8: 100 :: / 64. Устройству A не требуется пересчитывать свой путь к любому из узлов сети. Доступный пункт назначения - это просто лист дерева, даже если это набор хостов, подключенных к одному проводу (например, Ethernet). Нет причин пересчитывать весь SPT, когда один лист (или любой набор листьев) отключается от сети. В этом случае только лист (IP-адрес Интернет-протокола или доступный пункт назначения) должен быть удален из сети (или, скорее, пункт назначения может быть удален из базы данных без каких-либо изменений в сети). Это частичный пересчет SPT.
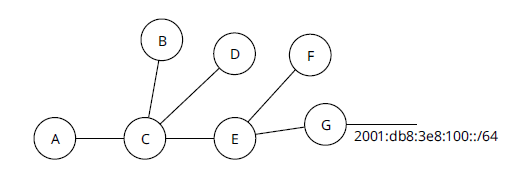
Предположим, что канал [C, E] не работает. Что делает А в этом случае? Опять же, топология C, B и D не изменилась, поэтому у A нет причин пересчитывать все дерево. В этом случае A может удалить все дерево за пределами E. Чтобы вычислить только измененную часть графа, выполните следующие действия:
- Удалите отказавший узел и все узлы, которые нужно достичь через точку E.
- Пересчитайте дерево только от предшественника C (в данном случае A), чтобы определить, есть ли альтернативные пути для достижения узлов, ранее доступных через E до того, как канал [C, E] не доступен.
Это называется инкрементным SPF.
Расчет LFA и rLFA.
Bellman-Ford не вычисляет ни соседей ниже по потоку, ни LFA, и, похоже, не располагает необходимой для этого информацией. DUAL по умолчанию вычисляет нисходящих соседей и использует их во время конвергенции. А как насчет протоколов на основе Дейкстры (и, соответственно, аналогичных алгоритмов SPF)? На рисунке 10 показан простой механизм, который эти протоколы могут использовать для поиска LFA и соседних узлов ниже по потоку.
Определение нисходящего соседа - это такое, при котором стоимость достижения соседом пункта назначения меньше, чем локальная стоимость достижения пункта назначения. С точки зрения А:
- A знает местную стоимость проезда к месту назначения на основе SPT, созданного с помощью SPF Дейкстры.
- A знает стоимость B и C, чтобы добраться до места назначения, вычитая стоимость каналов [A, B] и [A, C] из рассчитанной на местном уровне стоимости.
Следовательно, A может сравнивать локальную стоимость со стоимостью от каждого соседа, чтобы определить, находится ли какой-либо сосед в нисходящем направлении по отношению к любому конкретному месту назначения. Определение LFA:
Если затраты соседа для «меня» плюс затраты соседа на достижение пункта назначения ниже, чем местные затраты, соседом является LFA.
Вернее, учитывая:
- NC - это стоимость соседа до пункта назначения.
- BC - это стоимость соседа для меня.
- LC - местная стоимость до места назначения.
Если NC + BC меньше LC, то соседом является LFA. В этом случае A знает стоимость каналов [B, A] и [C, A] с точки зрения соседа (она будет содержаться в таблице топологии, хотя не используется при вычислении SPT с использованием алгоритма Дейкстры). Таким образом, LFA и нисходящие соседи требуют очень небольшой дополнительной работы для расчета, но как насчет удаленных LFA? Модель P/Q Space обеспечивает простейший способ для алгоритмов на основе Дейкстры вычисления соседних узлов и LFA. Рисунок 11 используется для иллюстрации изнутри P/Q Space.
Определение пространства P - это набор узлов, доступных с одного конца защищенного соединения, а определение пространства Q - это набор узлов, достижимых без пересечения защищенного канала. Это должно предложить довольно простой способ вычисления этих двух пространств с помощью Дейкстры:
Рассчитайте SPT с точки зрения устройства, подключенного к одному концу линии связи; удалить линию связи без пересчета SPT. Остальные узлы доступны с этого конца линии.
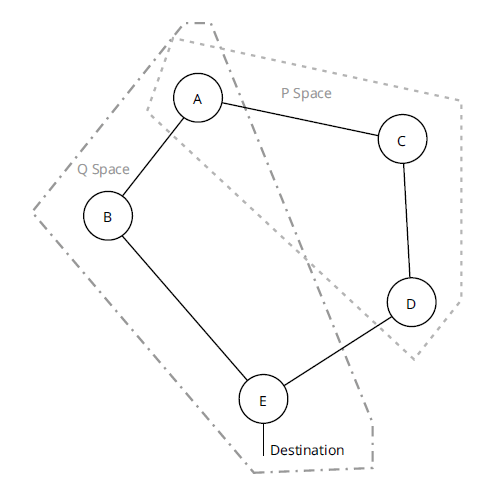
На рисунке 11 E может:
- Вычислите пространство Q, удалив линию [E, D] из копии локального SPT и всех узлов, для достижения которых E использует D.
- Вычислите пространство P, вычислив SPT с точки зрения D (используя D в качестве корня дерева), удалив линию [D, E], а затем все узлы, для достижения которых D использует E.
- Найдите ближайший узел, достижимый как из E, так и из D, с удаленной линией [E, D].
SPF Дейкстры - это универсальный, широко используемый алгоритм для вычисления Shortest Path Trees через сеть.
Получите бесплатные уроки на наших курсах
- Аналитик данных с нуля
- 1С-разработчик с нуля
- Redis для разработчиков и DevOps
- iOS-разработчик с нуля
- Системный аналитик с нуля



