
Алгоритм Дейкстра: Вектор пути
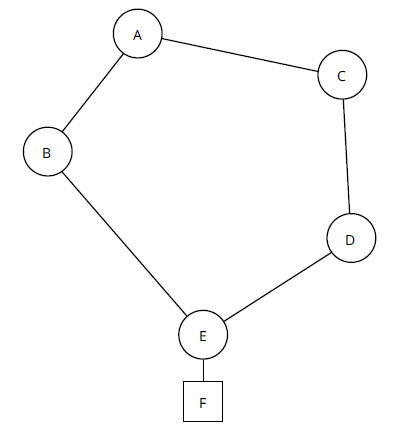
Вектор пути основан на хранении списка узлов, через которые проходит путь. Любой узел, который получает обновление с самим собой в пути, просто отбрасывает обновление, поскольку это не жизнеспособный путь. Рисунок 12 используется в качестве примера. На рисунке 12 каждое устройство объявляет информацию о местах назначения каждому соседнему устройству; для пункта назначения, прикрепленного к E:
- E будет анонсировать F с самим собой в источнике, поэтому с путем [E], как B, так и D.
- От B: B анонсирует F к A с путем [E, B].
- Из D: D анонсирует F в C с путем [E, D].
- От C: C анонсирует F к A с путем [E, D, C]
Какой путь предпочтет A? В системе вектора пути может быть ряд метрик, включая длину пути, предпочтения политики и т. д. Например, предположим, что есть метрика, которая устанавливается локально на каждом узле, переносимом с каждым маршрутом. Эта локальная метрика переносится между узлами, но никак не суммируется при прохождении через сеть, и каждый узел может устанавливать эту метрику независимо от других узлов (при условии, что узел использует одну и ту же метрику по отношению к каждому соседу). Например, локальная метрика E объявляется B, который затем устанавливает свою собственную локальную метрику для этого пункта назначения и объявляет результирующий маршрут A и т. д.
Чтобы определить лучший путь, каждый узел может затем
- Отбросить любое место назначения с идентификатором локального узла в пути.
- Сравнить метрику, выбрав наивысшую локальную метрику из полученных.
- Сравнить длину пути, выбрав самый короткий из полученных.
- Объявить только тот путь, который используется для пересылки трафика.
Примечание.Не имеет значения, выбирает ли каждый узел самую высокую или самую низкую метрику. Важно только то, что каждый узел выполняет одно и то же действие во всей сети. Однако при сравнении путей узел всегда должен выбирать более короткий путь.
Если каждый узел в сети всегда будет следовать этим трем правилам, то петля не образуется.
Например:
- E объявляет F в B с путем [E] и метрикой 100.
- B объявляет F к A с путем [E, B] и метрикой 100.
- E объявляет F в D с путем [E] и метрикой 100.
- D объявляет F в C с путем [E, D] и метрикой 100.
- C объявляет F в A с путем [E, D, C] и метрикой 100.
У A есть два пути, оба с одинаковой метрикой, и, следовательно, будет использовано второе правило, чтобы выбрать один путь, который является наиболее коротким. В этом случае A выберет путь через [E, B]. A будет объявлять маршрут, который он использует, к C, но если C следует тому же набору правил, у него также будет два пути с доступной метрикой 100, один с путем [E, B, A], а второй с путем [E, D, C]. В этом случае должен быть механизм разрешения конфликтов, который C использует внутри для выбора между двумя маршрутами. Неважно, что это за механизм разрешения конфликтов, если он постоянно применяется в узле. Независимо от того, какой путь выберет C, трафик к F не будет закольцован. Предположим, однако, несколько иное стечение обстоятельств:
- E объявляет F в B с путем [E] и метрикой 100.
- B объявляет F к A с путем [E, B] и метрикой 100.
- E объявляет F в D с путем [E] и метрикой 50.
- D объявляет F в C с путем [E, D] и метрикой 50.
- C объявляет F в A с путем [E, D, C] и метрикой 50.
У A есть два пути: один с метрикой 100, а другой с метрикой 50.
Следовательно:
- A выберет более высокую из двух метрик, путь через [E, B], и объявит этот маршрут C
- C выберет более высокую из двух метрик, путь через [E, B, A], и объявит этот маршрут D.
- D выберет более высокий из двух метрик, путь через [E, B, A, C], и объявит этот маршрут E.
- E отбросит этот маршрут, поскольку E уже находится на пути.
Следовательно, даже если метрика перекрывает длину пути в (почти) каждом узле, цикл не образуется.
Проблемы метрик
Каждый алгоритм, обсуждавшийся до этого момента, использовал одну метрику для вычисления путей без петель, за исключением вектора пути, а вектор пути использует две метрики очень ограниченным образом, причем одна всегда предпочтительнее другой. Путь, по сути, можно рассматривать как «фактор разрешения конфликтов», который вступает в игру только тогда, когда основная метрика, которая никак не связана с путем (поскольку она не суммируется шаг за шагом в сети), не соответствует предотвратить петлю. Некоторые протоколы могут использовать несколько метрик, но они всегда будут каким-то образом комбинировать эти метрики, поэтому для поиска путей без петель используется только одна комбинированная метрика. Почему?
С математической точки зрения, все методы, используемые для нахождения набора свободных от петель (или кратчайших) путей через сеть, разрешимы за полиномиальное или неэкспоненциальное время - или, скорее, они считаются проблемами класса P. Существует более широкий класс задач, содержащих P, который содержит любую задачу, решаемую с помощью (теоретической) недетерминированной машины Тьюринга. Среди NP-проблем есть набор задач, которые считаются NP-полными, что означает, что не существует известного эффективного способа решения проблемы. Другими словами, для решения проблемы необходимо перечислить все возможные комбинации и выбрать из этого набора наилучшее возможное решение.
Проблема с множественными метриками классифицируется как NP-complete, и, следовательно, хотя и разрешима, она никоим образом не решаема, что позволяет использовать ее в коммуникационных сетях, близких к реальному времени.
Алгоритмы непересекающихся путей
Рассмотрим ситуацию медицинской операции, выполняемой роботом, который следует за руками живого хирурга на другом конце света. Возможно, что для того, чтобы такая система работала, требуется, чтобы пакеты доставлялись от датчиков на руках хирурга к роботу в реальном времени, по порядку, с минимальным значением параметра jitter или без него, и никакие пакеты нельзя отбрасывать. Это один из примеров. Конечно, он может быть расширен для других различных ситуаций, включая финансовые системы и другие механические системы управления, где требуется доставка пакетов в реальном времени без сбоев.
В таких ситуациях часто требуется передать две копии каждого пакета, а затем позволить получателю выбрать пакет, наилучшим образом соответствующий характеристикам качества обслуживания (QoS) и потерям пакетов, необходимым для поддержки приложения. Однако все системы, рассмотренные до сих пор, могут найти только один путь без циклов и потенциально альтернативный путь (LFA и / или rLFA). Таким образом, с помощью алгоритмов непересекающихся путей решается следующая проблема:
Как можно построить пути в сети таким образом, чтобы они использовали наименьшее количество перекрывающихся ресурсов (устройств и каналов), насколько это возможно (следовательно, максимально непересекающиеся или максимально избыточные)?
В этой части лекций мы начнем с описания концепции двухсвязной сети, а затем рассмотрим два разных (но, казалось бы, связанных) способа вычисления непересекающихся топологий в двухсвязных сетях.
Двухсвязные сети
Двусвязная сеть - это любая сеть, в которой есть как минимум два пути между источником и местом назначения, которые не используют одни и те же устройства (узлы) или каналы (ребра). Обратите внимание на:
- Сеть является двусвязной по отношению к определенному набору источников и пунктов назначения; большинство сетей не имеют двух соединений для каждого источника и каждого пункта назначения.
- Небольшие блоки любой данной сети могут быть подключены двумя соединениями для некоторых источников и пунктов назначения, и эти блоки могут быть соединены между собой узкими одно- или двумя соединенными точками подключения.
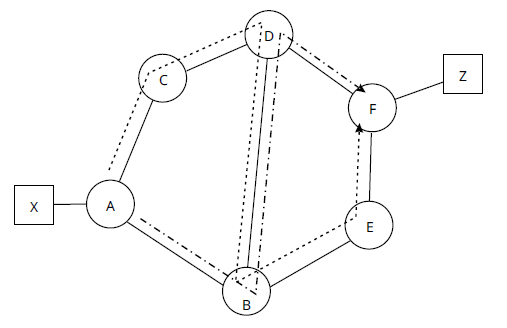
Часто проще всего понять двусвязность на реальном примере. На рисунке 13 показана сеть, с выделенными блоками.
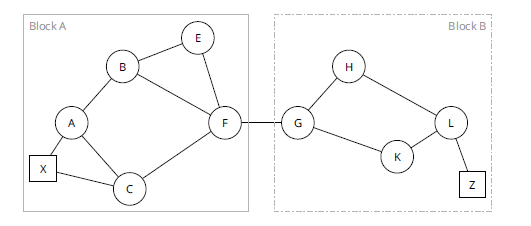
В блоке A есть как минимум два разных непересекающихся пути между X и F:
- [X, A, B, E, F] и [X, C, F]
- [X, A, B, F] и [X, C, F]
В блоке B есть одна пара непересекающихся путей из G в L: [G, K, L] и [G, H, L]. Непересекающихся путей к Z нет, так как этот узел односвязен. Между F и G также нет непересекающихся путей, так как они односвязны. Канал [F, G] можно рассматривать как узкую точку между этими двумя блоками топологии. В сети, показанной на рисунке 13, невозможно вычислить два непересекающихся пути между X и Z.
Алгоритм непересекающегося пути Суурбалле
В 1974 году Дж. Суурбалле опубликовал статью, описывающую, как использовать несколько запусков SPF-алгоритма Дейкстры для поиска нескольких непересекающихся топологий в сети. Алгоритм по существу вычисляет SPF один раз, удаляет подмножество линий, используемых в SPT, а затем вычисляет второй SPF по оставшимся линиям. Алгоритм Суурбалле труднее объяснить, чем проиллюстрировать на примере, поскольку он опирается на направленный характер связей, вычисляемых с помощью SPT. В качестве примеров используются рисунки 14-18.
На рисунке 14 показано состояние операций после завершения первого запуска SPF и вычисления начального SPT. Обратите внимание на стрелки направления на линиях. Не принято думать, что SPT является направленным, но на самом деле это так, когда каждая линия ориентирована в сторону от источника или корня дерева. Когда F вычисляет дерево обратно к X, оно также создает направленное дерево со стрелками, указывающими в противоположном направлении.
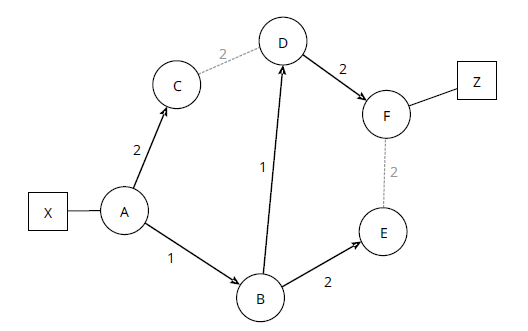
Ребра (или связи) на SPT называются ребрами дерева, а ребра (или связи), не входящие в результирующий SPT, называются ребрами не деревьев. На рис. 14 края дерева отмечены сплошным черным цветом со стрелками направления, а ребра не деревьев - более светлыми серыми пунктирными линиями.
Второй шаг показан на рисунке 15.
На рисунке 15 показано каждое звено с измененными затратами; каждая линия, которая была частью исходного SPT (каждое ребро дерева, показано сплошной линией), имеет две стоимости, по одной в каждом направлении, в то время как линии, которые изначально не были частью SPT (ребра, не входящие в состав дерева, показаны пунктирными линиями), имеют свои исходные расходы. Обратите внимание на стрелки, показывающие направление стоимости в каждом случае; это будет важно на следующем этапе расчета. Для расчета стоимости двух направленных линий для каждого ребра дерева:
- Именуем один конец линии символом u, а другой конец линии символом v. Обратите внимание, что уравнение выполняется в обоих направлениях.
- Вычтем стоимость источника до v из стоимости линии от u до v.
- Добавим стоимость из источника к u.
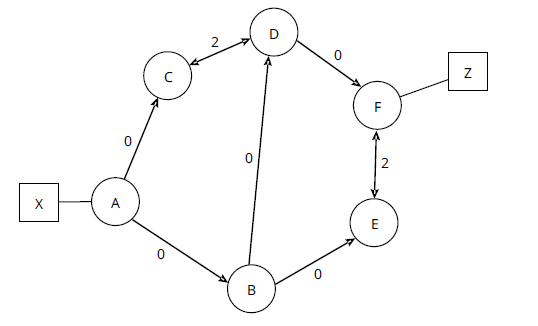
Если источник s: d[sp](u,v) = d(u,v) ? d(s,v) + d(s,u)
По сути, это устанавливает стоимость ребер дерева равной 0, как можно увидеть, выполнив математические вычисления для ссылки [B, E]:
- B - есть u, E - есть v, A - есть s
- d(u,v) = 2, d(s,v) = 3, d(s,u) = 1
- 2 ? 3 + 1 = 0
Однако для всех ребер, не входящих в дерево, будет установлена некоторая (обычно большая) ненулевая стоимость. Для сети на рисунке 15:
Для линии [B, A] (примечание [A, B] не является линией в вычисляемом дереве направлений):
- B - есть u, A - есть v, A - есть s
- d(u,v) = 0, d(s,v) = 0, d(s,u) = 1
- 0 ? 0 + 1 = 1
Для линии [E,B]:
- E – есть u, B – есть v, A - есть s
- d(u,v) = 2, d(s,v) = 1, d(s,u) = 3
- 2 ? 1 + 3 = 4
Для линии [C,A]:
- C – есть u, A – есть v, A – есть s
- d(u,v) = 2, d(s,v) = 0, d(s,u) = 2
- 2 ? 0 + 2 = 4
Для линии [F,D]:
- F – есть u, D – есть v, A – есть s
- d(u,v) = 1, d(s,v) = 4, d(s,u) = 5
- 1 ? 4 + 5 = 2
Для линии [D,B]:
- D – есть u, B – есть v, A – есть s
- d(u,v) = 1, d(s,v) = 1, d(s,u) = 2
- 1 ? 1 + 2 = 2
Следующий шаг, показанный на рисунке 16, состоит в том, чтобы удалить все направленные ребра, указывающие на источник, который лежит вдоль исходного SPT к определенному месту назначения (в данном случае Z), изменить направление ребер с нулевой стоимостью (линий) вдоль этого же пути, а затем снова запустить SPF Дейкстры, создав второй SPT на той же топологии.
Возвращаясь к исходному SPT, путь от X до Z проходил по пути [A,B,D,F]. Таким образом, четыре ненулевых ребра (пунктирные линии), указывающие назад к источнику, А, вдоль этого пути были удалены. Вдоль того же пути [A, B,D,F] направление каждого ребра было изменено. Например, [A,B] первоначально указывало от A к B, а теперь указывает от B к A. Следующий шаг-запустить SPF по этому графику, помня, что трафик не может течь против направления линии. Полученное дерево показано на рисунке 17.
На рисунке 17 показано исходное дерево и вновь вычисленное дерево, наложенные на исходную топологию в виде двух различных пунктирных линий. Эти две топологии все еще имеют общую связь [B,D], так что они еще не совсем разобщены. В этой точке есть два кратчайших пути от X до Z:
- [A,B,D,F]
- [A,C,D,B,E,F]

Эти два графа объединяются, образуя набор ребер, и любые связи, которые включены в оба графа, но в противоположных направлениях, отбрасываются; комбинированный набор выглядит так: [A->B, B->E, E->F, A->C, C->D, D->F]
Обратите внимание на направленность каждой линии связи еще раз - очень важно отсечь перекрывающуюся линию, которая будет указана как [B-> D] и [D-> B]. С помощью этого подмножества возможных ребер на графе можно увидеть правильный набор кратчайших путей: [A, B, E, F] и [A, C, D, F].
Алгоритм Суурбалле сложен, но показывает основные моменты вычисления непересекающихся деревьев, в том числе то, насколько сложно их вычислить.
Максимально избыточные деревья
Более простой альтернативой алгоритму Суурбалла для вычисления непересекающихся деревьев является вычисление максимально избыточных деревьев (Maximally Redundant Trees-MRT). Чтобы лучше понять MRT - это изучить Depth First Search (DFS), особенно нумерованный DFS. Рисунок 18 используется в качестве иллюстрации.
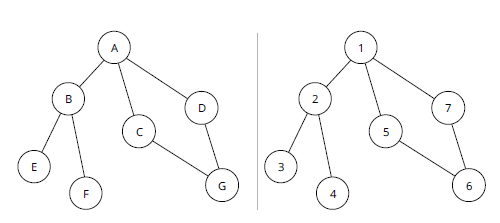
На рисунке 18 левая сторона представляет простую топологию. Правая-ту же топологию, которая была пронумерована с помощью DFS. Предполагая, что алгоритм DFS, используемый для «обхода» дерева, всегда выбирает левый узел над правым, процесс будет выглядеть примерно так:
01 main {
02 dfs_number = 1
03 root.number = dfs_number
04 recurse_dfs(root)
05 }
06 recurse_dfs(current) {
07 for each neighbor of current {
08 child = left most neighbor (not visited)
09 if child.number == 0 {
10 dfs_number++
11 child.number = dfs_number
12 if child.children > 0 {
13 recurse_dfs(child)
14 }
15 }
16 }
17 }
Лучший способ понять этот код-пройти рекурсию несколько раз, чтобы увидеть, как она работает. Используя рисунок 18:
- При первом вызове recurse_dfs в качестве текущего узла устанавливается A или root.
- Оказавшись внутри recurse_dfs, выбирается крайний левый узел A или B.
- B не имеет номера при входе в цикл, поэтому оператор if в строке 09 верен.
- B назначается следующий номер DFS (строка 11).
- У B есть дочерние элементы (строка 12), поэтому recurse_dfs вызывается снова с B в качестве текущего узла.
- Оказавшись внутри (второго уровня) recurse_dfs, выбирается крайний левый сосед B, которым является E.
- E не имеет номера DFS, поэтому оператор if в строке 09 верен.
- E назначается следующий номер DFS (3)
- E не имеет дочерних элементов, поэтому обработка возвращается к началу цикла.
- F теперь является крайним левым соседом B, который не был посещен, поэтому он назначен дочернему элементу.
- F не имеет числа, поэтому оператор if в строке 09 верен.
- F назначается следующий номер DFS (4).
- У B больше нет дочерних элементов, поэтому цикл for в строке 07 завершается ошибкой, и программа recurse_dfs завершается.
- Однако на самом деле recurse_dfs не выходит - он просто «возвращается» к предыдущему уровню рекурсии, то есть к строке 14. Этот уровень рекурсии все еще обрабатывает соседей A.
- C - следующий сосед A, который не был затронут, поэтому дочерний элемент установлен в C.
- И так далее
Изучение номеров узлов в правой части рисунка 18 приводит к следующим интересным наблюдениям:
- Если A всегда следует за возрастающим числом, чтобы достичь D,оно будет следовать по пути [A, C,G,D].
- Если D всегда следует за уменьшающимся числом DFS, чтобы достичь A,он будет следовать по пути [D, A].
- Эти два пути на самом деле не пересекаются.
Это свойство сохраняется для всех топологий, которым были присвоены номера в результате поиска DFS: путь, следующий за постоянно увеличивающимися числами, всегда будет не пересекаться с путем, который всегда следует за убывающими числами. Это именно то свойство, на котором MRT строят непересекающиеся пути. Однако проблема с нумерацией DFS заключается в том, что это трудно сделать почти в реальном времени. Должен быть какой-то избранный корень, трафик на локальном уровне неоптимален (во многом как Minimum Spanning Tree или MST), и любые изменения в топологии требуют перестройки всей схемы нумерации DFS. Чтобы обойти эти проблемы, MRT строит непересекающиеся топологии, используя тот же принцип, но другим способом. Рисунок 19 используется для пояснения.
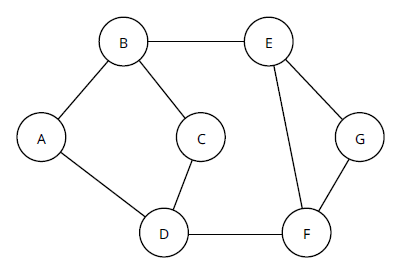
Первым шагом в построении MRT является поиск короткого цикла в топологии от корня (обычно эти петли обнаруживаются с помощью алгоритма SPF Дейкстры). В этом случае в качестве корня будет выбран A, а цикл будет [A, B, C, D]. Этот первый цикл будет использоваться как первая из двух топологий, скажем, красная топология. Обращение цикла к [A, D, C, B] создает непересекающуюся топологию, скажем, синюю топологию. Эта первая пара топологий через этот короткий цикл называется «ухом».
Для расширения диапазона МРТ к первому добавляется второе ухо. Для этого открывается второй цикл, на этот раз через [A, D, F, E, B], а непересекающаяся топология - [A, B, E, F, D]. Возникает вопрос: какое из этих двух расширений топологии следует добавить к красной топологии, а какое - к синей? Здесь вступает в игру форма нумерации DFS.
Каждому устройству в сети уже должен быть назначен идентификатор либо администратором, либо через какой-либо другой механизм. Эти идентификаторы должны быть уникальными для каждого устройства. В схеме нумерации DFS также существует концепция нижней точки, которая указывает, где на конкретном дереве прикрепляется этот узел, а также какие узлы присоединяются к дереву через этот узел.
Учитывая эти уникальные идентификаторы и возможность вычислять нижнюю точку, каждый узел в сети может быть упорядочен так же, как ему был присвоен номер в процессе нумерации DFS. Ключ в том, чтобы знать, как порядок соответствует существующей красной и синей топологиям. Предположим, что нижняя точка B выше, чем C, если топология [A, B, C, D] является частью красной топологии. Для любого другого «уха» или петли в топологии, которая проходит через B и C, направление «уха», в котором B меньше C, должно быть помещено в красную топологию. Петля в обратном направлении должна быть размещена на синей топологии. Это объяснение является довольно поверхностным, но оно дает вам представление о том, как MRT образуют непересекающиеся топологии.
Двусторонняя связь
В этой и предыдущей лекциях было описано несколько различных способов вычисления пути без петель (или набора непересекающихся путей) через сеть. В каждом из этих случаев вычисленный путь является однонаправленным - от корня дерева до краев или достижимых мест назначения. Фактически, обратного пути не существует. Другими словами, источник может иметь возможность достичь пункта назначения по пути без петель, но может не быть обратного пути от пункта назначения к источнику. Это может быть необычный режим отказа в некоторых типах каналов, результат фильтрации информации о доступности или ряд других ситуаций в сети.
Примечание. Двусторонняя связь не всегда нужна. Рассмотрим, например, случай с подводной лодкой, которая должна получать информацию о своей текущей задаче, но не может передавать какую-либо информацию, не раскрывая своего текущего местоположения. Желательна возможность отправлять пакеты устройствам, расположенным на подводной лодке, даже если к ним нет двусторонней связи. Плоскости управления должны быть модифицированы или специально спроектированы для обработки такого необычного случая, поскольку обычно для правильной работы сети требуется двустороннее соединение.
Еще одна проблема, с которой должны столкнуться плоскости управления в области вычислительных трактов, - это обеспечение сквозной двусторонней связи.
Уровень управления может решить эту проблему несколькими способами:
- Некоторые плоскости управления просто игнорируют эту проблему, что означает, что они предполагают, что какой-то другой протокол, например транспортный протокол, обнаружит это состояние.
- Плоскость управления может проверить наличие этой проблемы во время расчета маршрута. Например, при вычислении маршрутов с использованием алгоритма Дейкстры можно выполнить проверку обратной связи при вычислении путей без петель. Выполнение этой проверки обратной линии связи на каждом этапе вычислений может гарантировать наличие двусторонней связи.
- Плоскость управления может предполагать двустороннюю связь между соседями, обеспечивая сквозную двустороннюю связь. Плоскости управления, которые выполняют явные проверки двусторонней связи для каждого соседа, могут (как правило) безопасно предполагать, что любой путь через этих соседей также поддерживает двустороннюю связь.
Получите бесплатные уроки на наших курсах
- Data Science с нуля
- Android-разработчик с нуля
- Этичный хакинг
- MongoDB для разработчиков и DevOps
- Фронтенд с нуля



