.webp)
.webp)
В данной главе рассматриваются вопросы технической диагностики системы автоматического мониторинга ВОЛС, необходимость в которой возникает из-за сложности этой системы.
Техническое диагностирование - процесс определения технического состояния изделия с определенной точностью. Цель технического диагностирования это поддержание достаточного уровня надежности.
При наступлении отказа диагностирование предполагает обнаружение факта отказа и его локализацию. Система технического диагностирования (СТД) - совокупность средств, осуществляющих измерение количественных значений параметров (диагностических параметров ДП), анализ и обработку результатов измерений по установленным алгоритмам. Техническим средством диагностирования являются автоматические измерительные системы, рассмотренные в главе 2. Одним из основных методов решения задач диагностирования является моделирование объекта технического диагностирования и выделение взаимосвязей в этих моделях. Модель объекта - это формализованная сущность, характеризующая определенные свойства реального объекта в удобной и желательно для инженера в наглядной форме.
Существуют аналитические модели, в которых модель строится на основе уравнений, связывающих различные параметры; графоаналитические, основанные на представлении диаграмм (в частности направленных графов) прохождения сигналов; информационные модели представляют собой информационные описания в терминах энтропия, информация и т.п.
Чаще всего используемым в практических целях и наиболее наглядным являются функционально-логические модели, которые реализуются различными способами, определяемыми особенностью функциональной схемы диагностируемого изделия.
В настоящей работе применяется диагностирование, основанное на функционально-логическом моделировании и реализуемое инженерным способом. В соответствии с решаемой задачей выбирается та или иная "функция предпочтения". В данном случае решается задача поиска неисправности, для которой выбирается W4 функция предпочтения о которой ниже.
Разработка алгоритма диагностирования
Считаем, что объект диагностирования задан следующей функциональной схемой (рисунок 1).
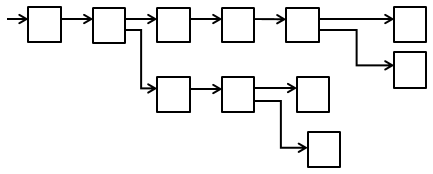
После построения функциональной модели необходимо определить множество возможных состояний объекта, который диагностируется. Общее число состояний при N функциональных элементов при двоичных исходах проверок (1 исправно, 0 неисправно) равно при диагностировании системы 2N - 1. Предполагается, что одновременное появление двух независимых отказов маловероятно, поэтому число сочетаний из N элементов по одному, равно N. Число всех возможных различных состояний аппаратуры, которая диагностируется, одновременно с учетом отказов одного функционального - сводятся в таблицу состояний (матрицу исправностей, матрицу неисправностей и т. п.), которая используется при разработке программы (алгоритма) поиска неисправностей.
Матрица состояний строится по следующим правилам:
- S0 - строка, соответствующая работоспособному состоянию;
- Sj - строка, соответствующая состоянию в котором оказался j-тый элемент модели.
Например, состояние S4 = 0 означает событие, при котором отказал 4-ый четвертый элемент модели; S2 = 0- второй и т.п.). Этому событию соответствует недопустимое значение сигнала Zi, и тогда на пересечении 
пишется 0. Если любой другой i - й элемент также недопустимое значение Zi, то на пересечении j ой строки и Zi - ого столбца таким же образом записывается "0"; при этом, если значение параметра будет находиться в допуске, то на пересечении 
пишется "1". Считается, что значения всех внешних входных сигналов xi всегда будут находиться в пределах допуска, а линии связи между элементами абсолютно надежны. Если есть сомнение в надежности линии, то её принимают за функциональный элемент.
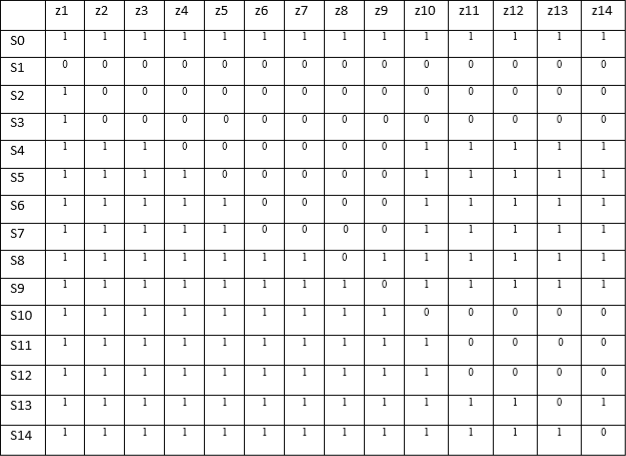
Транспонируем матрицу (таблица 1). Так как мы осуществляем построение алгоритма поиска неисправности, то первую строку S0, означающее исправное состояние исключаем. Последний столбец функция предпочтения W4, которую установили из следующих соображений.
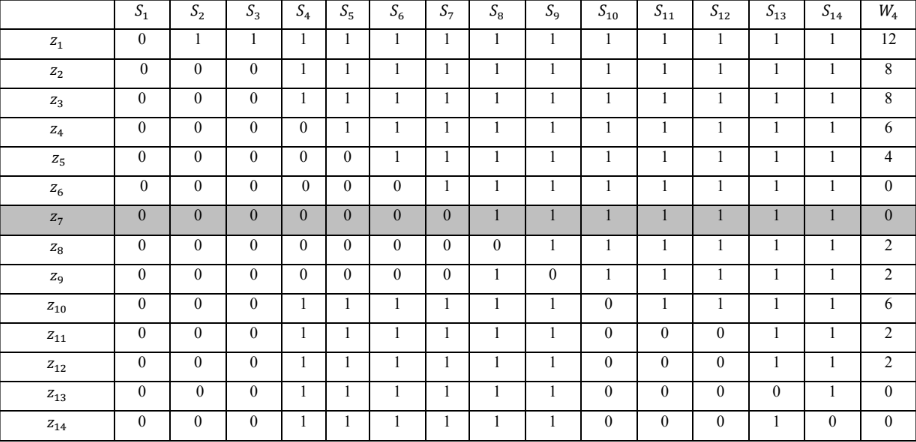
Так как матрица заполнена нулями и единицами, то равенство некоторого ij элемента соответствует тому, отказ i-го элемента влияет на j-ый выходной параметр j-го элемента, если контролировать выходной параметр Zj можно определить, в каком именно состоянии находится i-ый элемент. Следовательно, чем больше "0" в строке Zj матрицы, тем более большое количество информации может нести этот параметр о состоянии объекта, который находится под контролем. Для этого в качестве предпочтительной функции решении данной задачи контроля работоспособности необходимо принимать функцию вида:
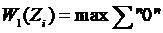
Где 
;
- означает количество нулей в I-ой строке матрицы.
Если для объекта контроля известны вероятности состояний P(Zi):
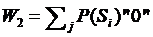
Также заданы C(Zi) стоимости контроля параметров:
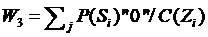
Так как строится алгоритм нахождения неисправности, то функция предпочтения будет:
где суммы означают количество нулей и единиц соответственно в I-той строке транспонированной матрицы состояний. Значения W4(Zi) для каждой строки приведены в последнем столбце транспонированной матрицы (таблица 3.2).
Последовательность решения следующая:
- 1) Выбираем ту строку, в которой функция предпочтения W4(Zi) минимальна, так как эта строка несет максимальное количество информации, разбивая все возможные состояния объекта на две равные части.
- 2) Минимально значение для 6,7,13 и 14 строк, т.е. по этому критерию они равнозначны. Для контроля выбираем строку 7. Итог контроля по этому параметру W4(Zi) разбивает матрицу на равные части W4(Z7) - первое разложение:
- 2.1) Эти состояния не влияют на данный выходной параметр функционального элемента;
- 2.2) Значения параметра не в допуске, что говорит о неисправности объекта.
- 3) Дальше аналогично анализируются обе получившиеся части (3-е, 4-е и последующие разложения (как показано на рисунке 6).
- 4) Процедура продолжается, пока множество N=14 возможных состояний объекта диагностирования не будут разделены на отдельные состояния.
Чтобы упорядочить для дальнейшего осколки введём следующее обозначение для каждого конкретного осколка: 
Где m - номер разбиения;
"H" - принимает значение 1 или 0 в зависимости от состояния строки матрицы;
n - номер осколка, считая, что осколки всегда располагаются, начиная с "1".
Например, обозначение 3«0»6 значит, что это осколок при третьем разбиении для значения "0". (впрочем, "1" всегда соответствуют нечетные значения "n", а «0» - четные)
Ниже представлены результаты анализа для принятой конкретной функциональной модели на рисунке 3.
Первое разбиение по строке Z7, имеющая W7 = 0
z7, имеющая W7 = 0
В таблице 3.3. представлена матрица (осколок) после первого разбиения для результатов проверки «1», т.е. при введенных обозначениях: 1«1»1. Для второго разбиения взята строка Z11, имеющая меньшее значение функции предпочтения W4 = 1
В таблице 3.4 представлена таблица после первого разбиения с «0»,, т.е. 1«0»,1.
Дальше "заливкой" показаны строчки, выбранные для следующих разбиений.
Для первого разбиения матрицы взята строка Z11, функция предпочтения которой W4 = 1.
|
S8 |
S9 |
S10 |
S11 |
S12 |
S13 |
S14 |
W4 |
|
|
z8 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
5 |
|
z9 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
5 |
|
z10 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
5 |
|
z11 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
z12 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
z13 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
z14 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
Таблица 3. - 1«1»1
|
S1 |
S2 |
S3 |
S4 |
S5 |
S6 |
S7 |
W4 |
|
|
z1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
5 |
|
z2 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
z3 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
z4 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
z5 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
3 |
|
z6 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
7 |
|
z7 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
7 |
Таблица 4. - 1«0»1
Матрица после второго разбиения при «1». Для 3-го разбиения взята строка Z13
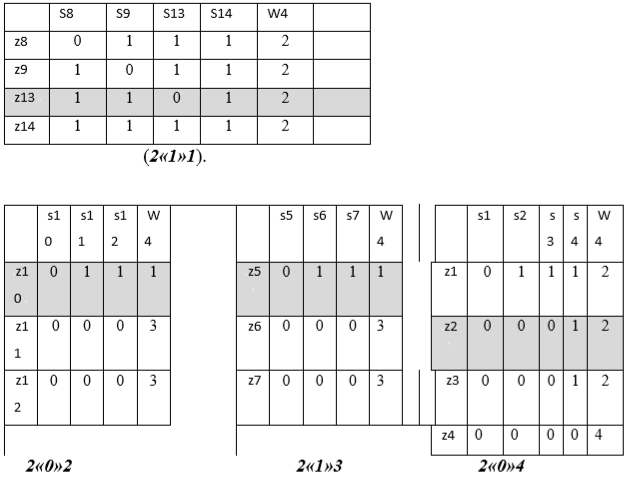
Результаты третьего разбиения:
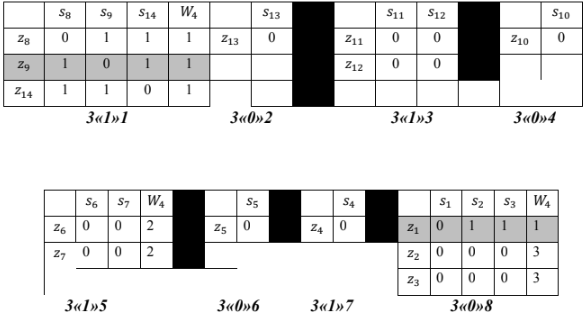
Результаты четвертого разбиения:
По результатам разбиений получаем номера ФБ для контроля:
результат третьего разбиения:
- 3«0»2→13;
- 3«1»4→11 и 12;
- 3«0»4→10;
- 3 «1»5→6 и 7;
- 3«0»6→5;
- 3 «1»7→4.
Результат четвертого разбиения:
- 4«0»2 → 9.
Результат пятого разбиения:
- 5«1»1 → 8;
- 5«0» →14;
- 5«1»15 → 2 и 3;
- 5«0»16 →1.
По полученным в результате анализа матрицы состояний номерам контролируемых ФБ для определения неисправного блока строим алгоритм контроля.
Алгоритм контроля
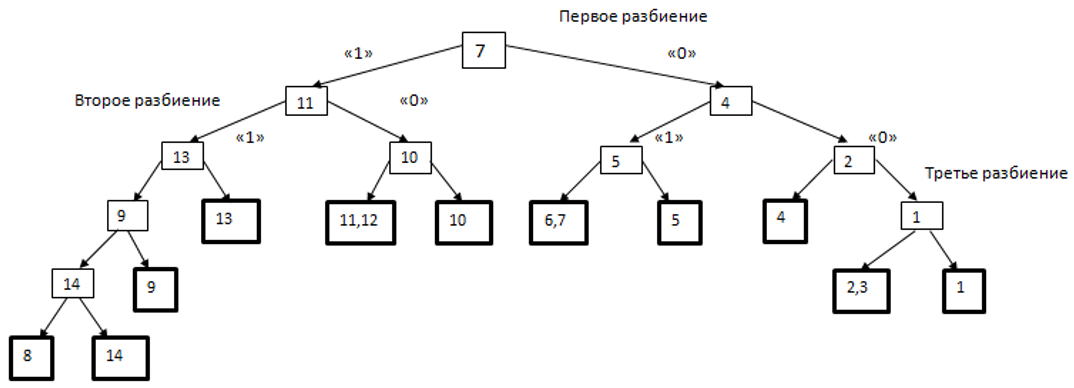
Рисунок 2. Как видно из алгоритма, максимальное количество элементарных проверок для нахождения неисправного ФБ равно 5 (в данном случае ФБ 8 и 14)
Заключение
- 1.На основе функционально-логической модели и инженерного способа разработан оптимальный алгоритм диагностирования гипотетической систем, которая моделирует систему автоматического контроля и мониторинга.
- 2. Проведен расчет и в результате получен алгоритм. Для принятой модели максимальное число элементарных испытаний равно 5.
