А пока не начали - почитайте материал про одноадресные пути без петель.
Простое правило кратчайшего пути используется для построения описания набора путей, а не одного пути в реальных сетях. Хотя для представления набора путей через топологию или сеть можно использовать ряд различных видов деревьев, для описания компьютерных сетей обычно используются два: Minimum Spanning Tree - MST и Shortest Path Tree - SPT. Разница между этими двумя видами деревьев часто неуловима. Сеть, показанная на рисунке 3, будет использоваться для иллюстрации MST и SPT.
На рисунке 3 несколько различных путей будут касаться каждого узла, например, с точки зрения А:
- [A, B, E, D, C] и [A, C, D, E, B], каждая общей стоимостью 10
- [A, B, E] стоимостью 5 и [A, C, D] стоимостью 3, общая стоимость 8
- [A, C, D, E] стоимостью 6 и [A, B] стоимостью 1, общая стоимость - 7
MST - это дерево, которое посещает каждый узел в сети с минимальной общей стоимостью (обычно измеряется как сумма всех линий связи, выбранных в сети).
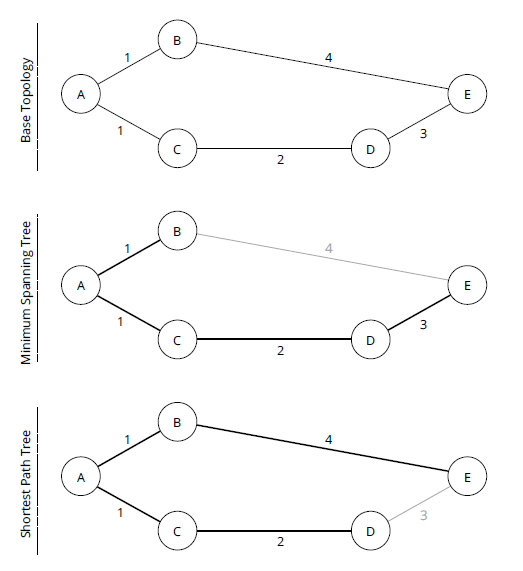
Алгоритм, вычисляющий MST, выберет вариант 3, поскольку он имеет наименьшую общую стоимость по набору граней, необходимых для достижения каждого узла в сети.
SPT описывает кратчайший путь к каждому пункту назначения в сети, независимо от общей стоимости графа. Алгоритм, вычисляющий SPT, с точки зрения A выбрал бы:
- От [A, B] до B со стоимостью 1, так как этот путь короче, чем [A, C, D, E, B] со стоимостью 10
- [A, B, E] в E стоимостью 5, так как это короче, чем [A, C, D, E] стоимостью 6
- От [A, C] до C со стоимостью 1, так как это короче, чем [A, B, E, D, C] со стоимостью 10
- [A, C, D] в D стоимостью 3, так как это короче, чем [A, B, E, D] стоимостью 8
Сравнивая набор кратчайших путей с набором путей, которые будут касаться каждого узла, приведенный выше алгоритм, вычисляющий SPT, выберет вариант 2, а не 3 в вышеуказанном списке. Другими словами, SPT будет игнорировать общую стоимость граней в MST, чтобы найти кратчайший путь к каждому достижимому месту назначения (в данном случае к узлам), тогда как MST будет игнорировать кратчайший путь к каждому достижимому месту назначения, чтобы минимизировать стоимость всего графа.
Плоскости управления сетью чаще всего вычисляют SPT, а не MST, используя какую-либо форму greedy алгоритма. Хотя SPT не оптимальны для решения всех проблем, связанных с потоками сетевого трафика, они, как правило, лучше, чем MST, в типах проблем потока трафика, которые должны решать плоскости управления сетью.
Greedy алгоритм
Greedy алгоритмы выбирают локально оптимальные решения для решения больших проблем. Например, при вычислении кратчайшего пути через сеть Greedy алгоритм может выбрать посещение более близких соседних узлов (может быть достигнуто через линию связи с более низкой стоимостью) перед узлами, которые находятся дальше (могут быть достигнуты через линию связи с более высокой стоимостью). Таким образом, можно сказать, что Greedy алгоритмы ослабляют вычисления, обычно игнорируя или приближая глобальную оптимизацию.
Иногда Greedy алгоритмы могут потерпеть неудачу. Когда они действительно дают сбой, они могут потерпеть впечатляющую неудачу, обеспечивая худшее из возможных решений. Например, при правильном наборе метрик жадный алгоритм, такой как алгоритм Дейкстры, может вычислить набор самых длинных путей через сеть, а не набор самых коротких. Поэтому Greedy алгоритмы иногда считаются эвристическими, поскольку они приближают решение сложной задачи или могут решить ее в ограниченных средах, а не фактически решают общую задачу.
В реальном мире компьютерные сети спроектированы таким образом, чтобы эти алгоритмы вычисляли наилучшее возможное решение поставленной проблемы в каждом случае, а именно нахождение кратчайшего набора путей через сеть.
А дальше интереснее - почитайте про альтернативные пути без петель.
