Все мы любим компьютеры. Они могут делать столько удивительных вещей. За пару десятилетий компьютеры произвели самую настоящую революцию почти во всех аспектах человеческой жизни.
Они могут справляться с задачами различной степени сложности, просто переворачивая нули и единицы. Просто удивительно, как такое простое действие может привести к такому уровню сложности.
Но я уверен, что вы все знаете, что такой сложности нельзя добиться (практически нельзя) простым случайным переворачиванием чисел. Но за этим стоит определенные логические рассуждения. Есть правила, которые определяют, как это все должно происходить. В данной статье мы обсудим эти правила и увидим, как они управляют «мышлением» компьютера.
Что такое булева алгебра?
Это правила, о которых я упоминал выше, описываются некой областью математики, называемой булевой алгеброй.
В своей книге 1854 года британский математик Джордж Буль предложил использовать систематический набор правил для работы со значениями истинности. Эти правила положили математическую основу для работы с логическими высказываниями. А эти основы привели к развитию булевой алгебры.
Для того, чтобы понять, что из себя представляет булева алгебра, сначала мы должны понять сходства и различия между ней и другими формами алгебры.
Алгебра в целом занимается изучением математических символов и операций, которые можно выполнять над этими символами.
Эти символы сами по себе ничего не значат. Они обозначают некую величину. Именно эти величины и придают ценность этим символам, и именно с этими величинами и выполняются операции.
Булева алгебра также имеет дело с символами и правилами, позволяющими выполнять различные операции над этими символами. Разница заключается в том, что эти символы что-то значат.
В случае обычной алгебры символы обозначают действительные числа. А в булевой алгебре они обозначают значения истинности.
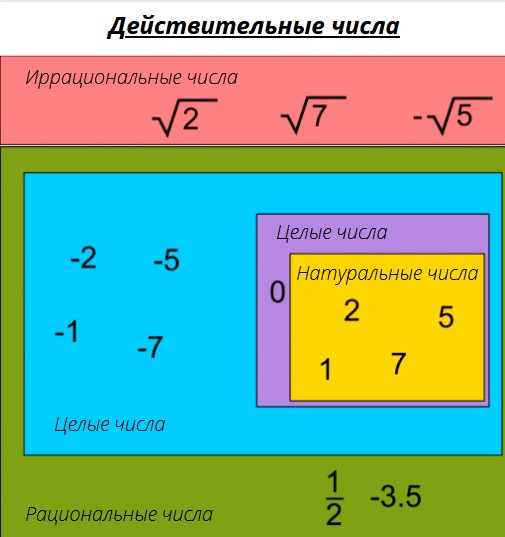
На рисунке ниже представлен весь набор действительных чисел. Набор действительных чисел включает натуральные числа (1, 2, 3, 4, …), положительные целые числа (все натуральные числа и 0), целые числа (…, -2, -1, 0, 1, 2, 3, …) и т.д. Обычная алгебра имеет дело со всем этим набором чисел.
Для сравнения, значения истинности состоят из набора, который включает в себя только два значения: True и False. Здесь я хотел бы отметить, что мы можем использовать любые другие символы для обозначения этих значений.
Например, в информатике, как правило, эти значения обозначают через 0 и 1 (0 используется в качестве False, 1 – в качестве True).
Вы также можете сделать это более оригинальным способом, обозначая значения истинности какими-то другими символами, например, кошки и собаки или бананы и апельсины.
Суть здесь в том, что смысл этих значений останется неизменным, как бы вы их не обозначили. Но убедитесь, что вы не меняете символы в процессе выполнения операций.
Теперь вопрос в том, что если (True и False), (0 и 1) – это просто обозначения, то что же они пытаются обозначить?
Смысл, лежащий в основе значений истинности, исходит из области логики, где значения истинности используются для того, чтобы определить, является ли высказывание «Истинным» (True) или «Ложным» (False). Здесь значения истинности обозначают соответствие высказывания истине, то есть показывают, является ли высказывание истинным или ложным.
Высказывание – это просто некоторое утверждение, что-то вроде «Все кошки милые».
Если приведенное выше высказывание верно, то мы присваиваем ему значение истинности «Истина» (True) или «1», в противном случае мы присваиваем ему значение истинности «Ложь» (False) или «0».
В цифровой электронике значения истинности используются для обозначения состояний электронных схем «включено» и «выключено». Подробнее об этом мы поговорим позже в этой же статье.
Логические операции и таблицы истинности
Как и в обычной алгебре, в булевой алгебре также можно применять операции к значениям для получения некоторых результатов. Однако эти операции не похожи на операции в обычной алгебре, поскольку, как мы уже упоминали ранее, булева алгебра работает со значениями истинности, а не с действительными числами.
В булевой алгебре есть три основные операции.
OR: OR или "ИЛИ", также известная как дизъюнкция. Эта операция выполняется над двумя логическими переменными. Результатом операции OR будет 0, если оба операнда равны 0, иначе будет 1.
Для того, чтобы более наглядно продемонстрировать принцип работы этой операции, визуализируем ее с помощью таблицы истинности.
Таблицы истинности дают нам хорошее представление о том, как работают логические операции. Также это удобный инструмент для выполнения логических операций.
Операция OR:
| Переменная 1 | Переменная 2 | Результат |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
AND: AND или "И", также известная как конъюнкция. Эта операция выполняется над двумя логическими переменными. Результатом операции AND будет 1, если оба операнда равны 1, иначе будет 0. Таблица истинности выглядит следующим образом.
Операция AND:
| Переменная 1 | Переменная 2 | Результат |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
NOT: NOT или "НЕ", также известное как отрицание. Эта операция выполняется только над одной переменной. Если значение переменной равно 1, то результатом этой операции будет 0, и наоборот, если значение переменной равно 0, то результатом операции будет 1.
Операция NOT:
| Переменная 1 | Результат |
| 0 | 1 |
| 1 | 0 |
Булева алгебра и цифровые схемы
Булева алгебра после своего появления очень долго оставалась одним из тех понятий в математике, которые не имели какого-то значительного практического применения.
В 1930-х годах Клод Шеннон, американский математик, обнаружил, что булеву алгебру можно использовать в схемах, где двоичные переменные могут обозначать сигналы «низкого» и «высокого» напряжения или состояния «включено» и «выключено».
Эта простая идея создания схем с помощью булевой алгебры привела к развитию цифровой электроники, которая внесла большой вклад в разработку схем для компьютеров.
Цифровые схемы реализуют булеву алгебру при помощи логических элементов – схем, обозначающих логическую операцию. Например, элемент OR будет обозначать операцию OR. То же самое относится и к элементам AND и NOT.
Наряду с основными логическими элементами существуют и логические элементы, которые можно создать путем комбинирования основных логических элементов.
NAND: элемент NAND, или "И-НЕ", образован комбинацией элементов NOT и AND. Элемент NAND дает на выходе0, если на обоих входах 1, в противном случае – 1.
Элемент NAND обладает свойством функциональной полноты. Это означает, что любая логическая функция может быть реализована только с помощью элементов NAND.
Элемент NAND:
| Вход 1 | Вход 2 | Результат |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOR: элемент NOR, или "ИЛИ-НЕ", образован комбинацией элементов NOT и OR. Элемент NOR дает на выходе 1, если на обоих входах 0, в противном случае – 0.
Элемент NOR, как и элемент NAND, обладает свойством функциональной полноты. Это означает, что любая логическая функция может быть реализована только с помощью элементов NOR.
Элемент NOR:
| Вход 1 | Вход 2 | Результат |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Большинство цифровых схем построены с использованием элементов NAND и NOR из-за их функциональной полноты, а также из-за простоты изготовления.
Помимо элементов, рассмотренных выше, существуют также особые элементы, которые служат для определенных целей. Вот они:
XOR: элемент XOR, или "исключающее ИЛИ", - это особый тип логических элементов, который дает на выходе 0, если оба входа равны 0 или 1, в противном случае – 1.
Элемент XOR:
| Вход 1 | Вход 2 | Результат |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
XNOR: элемент XNOR, или "исключающее ИЛИ-НЕ", - это особый тип логических элементов, который дает на выходе 1, когда оба входа равны 0 или 1, в противном случае – 0.
Элемент XNOR:
| Вход 1 | Вход 2 | Результат |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Заключение
Итак, на этом мы можем закончить обсуждение булевой алгебры. Надеюсь, что к текущему моменту у вас сложилась неплохая картина того, что же такое булева алгебра. Это, конечно, далеко не все, что вам следует знать о булевой алгебре. В ней есть множество понятий и деталей, которые мы не обсудили в данной статье.