Bellman-Ford - один из наиболее простых для понимания протоколов, поскольку он обычно реализуется путем сравнения недавно полученной информации о пункте назначения с существующей информацией о том же пункте назначения. Если вновь обнаруженный маршрут лучше, чем известный в настоящее время, маршрут с более высокой стоимостью просто заменяется в списке путей - в соответствии с правилом кратчайшего пути для поиска путей без петель в сети. Таким образом, перебирая всю топологию, можно найти набор кратчайших путей к каждому месту назначения. Рисунок 7 используется для иллюстрации этого процесса.

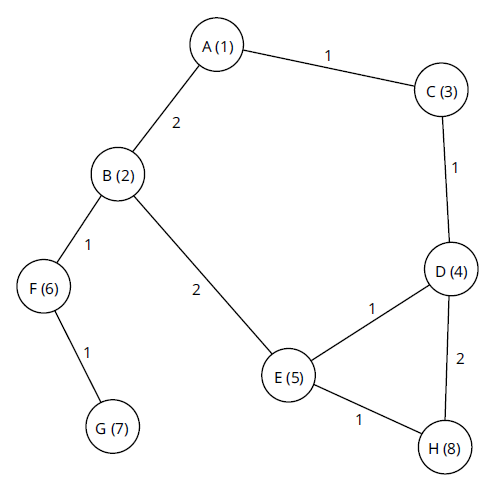
Расчет пути Bellman-Ford без петель
Примечание. Хотя Bellman-Ford в основном известен своим распределенным вариантом, реализованным в широко распространенных протоколах, таких как Routing Information Protocol (RIP), он изначально был разработан как алгоритм поиска, выполняемый в единой структуре, описывающей топологию узлов и ребер. Беллман-Форд рассматривается здесь как алгоритм.
Алгоритм Bellman-Ford
Bellman-Ford рассчитывает Shortest Path Tree к каждому достижимому пункту назначения в наихудшем случае O (V * E), где V - количество узлов (вершин) в сети, а E - количество каналов (ребер). По сути, это означает, что время, необходимое Bellman-Ford для работы с топологией и вычисления Shortest Path Tree, линейно зависит от количества устройств и каналов. Удвоение количества любого из них удвоит время, необходимое для выполнения. Удвоение обеих одновременно увеличит время работы в 4 раза.
Таким образом, алгоритм Bellman-Ford является умеренно медленным при использовании против более крупных топологий, когда узлы в таблице топологии начинаются в порядке от самого дальнего от корня до ближайшего к корню. Если таблица топологии отсортирована от ближайшего к корню до самого дальнего, Bellman-Ford может завершить работу за O(E), что намного быстрее. В реальном мире трудно обеспечить любой порядок, поэтому фактическое время, необходимое для построения Shortest Path Tree, обычно находится где-то между O(V * E) и O(E).
Bellman-Ford - это greedy алгоритм, предполагающий, что каждый узел в сети, кроме локального, доступен только по бесконечным стоимостям, и заменяющий эти бесконечные стоимости фактическими стоимостями по мере прохождения топологии. Предположение, что все узлы бесконечно удалены, называется ослаблением вычислений, так как он использует приблизительное расстояние для всех неизвестных пунктов назначения в сети, заменяя их реальной стоимостью после ее расчета.
Фактическое время выполнения любого алгоритма, используемого для расчета Shortest Path Tree, обычно ограничивается количеством времени, требуемым для передачи информации об изменениях топологии по сети. Реализации всех этих протоколов, особенно в их распределенной форме, будут содержать ряд оптимизаций, чтобы сократить время их выполнения до уровня, намного меньшего, чем наихудший случай, поэтому, хотя наихудший случай дается в качестве контрольной точки, он часто имеет мало влияющие на производительность каждого алгоритма в реальных развернутых сетях.
Чтобы запустить алгоритм Bellman-Ford в этой топологии, ее необходимо сначала преобразовать в набор векторов и расстояний и сохранить в структуре данных, такой как показано в Таблице 1.
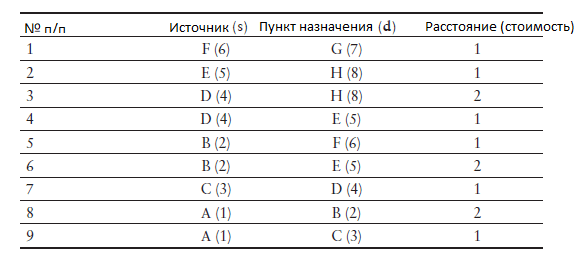
В этой таблице девять записей, потому что в сети девять звеньев (граней). Алгоритмы кратчайшего пути вычисляют однонаправленное дерево (в одном направлении вдоль графа). В сети на рисунке 7 показано, что SPT берет начало в узле 1, а расчет показан удаленным от узла 1, который будет точкой, из которой будут выполняться вычисления. Алгоритм в псевдокоде следующий:
// создаем набор для хранения ответа, по одной записи для каждого узла
// первый слот в результирующей структуре будет представлять узел 1,
// второй узел 2 и т. д.
define route[nodes] {
predecessor // как узел
cost // как целое число
}
// установите для источника (меня) значение 0
// позиция 1 в массиве - это запись исходной точки.
route[1].predecessor = NULL
route[1].cost = 0
// таблица 1, приведенная выше, содержится в массиве под именем topo
// Обходим таблицу вершин (граней) один раз для каждой записи в маршруте
// (результаты) таблица, замены более длинных записей на более короткие
i = nodes
while i > 0 {
j = 1
while j <= nodes { // перебирает каждую строку в топологии
table
source_router = topo[j].s
destination_router = topo[j].d
link_cost = topo[j].cost
if route[source_router].cost == NULL {
source_router_cost = INFINITY
} else {
source_router_cost = route[source_router].cost
}
if route[destination_router].cost == NULL {
destination_router_cost = INFINITY
} else {
destination_router_cost = route[destination_router].cost
}
if source_router_cost + link_cost <= destination_router_cost {
route[destination_router].cost = source_router_cost + link_
cost
route[destination_router].predecessor = source_router
}
j = j + 1 //or j++ depending on what pseudocode this is
representing
}
i = i - 1
}
Этот код обманчиво выглядит сложнее, чем есть на самом деле. Ключевой строкой является сравнение if route [topo [j] .s] .cost + topo [j] .cost route [topo [j] .d] .cost. Полезно сосредоточиться на этой строке в примере. При первом прохождении внешнего цикла (который выполняется один раз для каждой записи в таблице результатов, здесь называется маршрутом):
- Для первой строки topo-таблицы:
- j равно 1, поэтому topo[j] .s - это узел 6 (F), источник вектора в таблице граней
- j равно 1, поэтому topo[j] .d - это узел 7 (G), адресат вектора в таблице граней.
- route[6].cost = infinity, topo[1].cost = 1, and route[7].cost = infinity (где infinity - бесконечность)
- infinity + 1 == infinity, поэтому условие не выполняется и больше ничего не происходит
- Любая запись в topo-таблице с исходной стоимостью infinity даст тот же результат, что и infinity + все, что всегда будет равно infinity. Остальные строки, содержащие источник со стоимостью infinity, будут пропущены.
- Для восьмой строки topo-таблицы (восьмая грань):
- j равно 8, поэтому topo[j].s - это узел 1 (A), источник вектора в таблице граней
- j равно 8, поэтому topo[j].d - это узел 2 (B), место назначения вектора в таблице граней.
- route [1].cost = 0, topo[8].cost=2 и route[2].cost = infinity.
- 0 + 2 = infinity, поэтому условие выполняется
- route[2].predecessor установлен на 1, а route [2].cost установлен на 2
- Для девятой строки topo -таблицы (девятая грань):
- j равно 9, поэтому topo[j].s - это узел 1 (A), источник вектора в таблице граней
- j равно 9, поэтому topo[j].d - это узел 3 (C), место назначения вектора в таблице граней.
- route[1].cost=0, topo[9].cost=1 и route[3].cost = infinity.
- 0 + 1 = infinity, поэтому условие выполняется
- route[3].predecessor установлен на 1, а route[3].cost установлен на 1
Во втором прогоне внешнего цикла:
- Для пятой строки topo-таблицы (пятая грань):
- j равно 5, поэтому topo[j].s - это узел 2 (B), источник вектора в таблице граней
- j равно 5, поэтому topo[j].d - это узел 6 (F), место назначения вектора в таблице граней.
- route[2].cost=2,topo[5].cost=1 и route[6].cost = infinity.
- 2 + 1 = infinity, поэтому условие выполняется
- route[6].predecessor установлен на 2, а route[6].cost установлен на 3
Для шестой строки topo -таблицы (шестая грань):
- j равно 6, поэтому topo[j].s равно 2 (B), источник вектора в таблице граней
- j равно 6, поэтому topo[j].d равно 5 (E), место назначения вектора в таблице граней
- route[2].cost=2, topo[6].cost=2 и route[5].cost = infinity.
- 2 + 2 = infinity, поэтому условие выполняется
- route[5].predecessor установлен на 2, а route[5].cost установлен на 4
- Окончание этого прогона показан в Таблице 2.
В третьем прогоне внешнего цикла узел 8 представляет особый интерес, поскольку есть два пути к этому месту назначения. Для второй строки topo -таблицы (вторая грань):
- j равно 2, поэтому topo[j].s - это узел 5 (E), источник вектора в таблице граней
- j равно 2, поэтому topo[j].d - это узел 8 (H), место назначения вектора в таблице граней
- route[5].cost=4, topo[2].cost=1 и route[8].cost = infinity.
- 4 + 1 = infinity, поэтому условие выполняется
- route[8].predecessor установлен на 5, а route[8].cost установлен на 5
Для третьей строки topo -таблицы (третья грань):
- j равно 3, поэтому topo[j].s - это узел 4 (D), источник вектора в в таблице граней
- j равно 3, поэтому topo[j].d - это узел 8 (H), источник вектора в таблице граней
- route[4].cost=2,topo[3].cost=2 и route[8].cost = 5.
- 2 + 2 = 4, поэтому условие выполняется
- route[8].predecessor установлен на 4, а route[8].cost установлен на 4
Интересным моментом в третьем цикле в topo-таблице является то, что запись для грани [5,8] обрабатывается первой, которая устанавливает передатчик 8 (H) на 5 и стоимость на 5. Однако когда обрабатывается следующая строка в таблице topo [4,8], алгоритм обнаруживает более короткий путь к узлу 8 и заменяет существующий. Таблица 2 показывает состояние таблицы маршрутов при каждом проходе через таблицу topo.
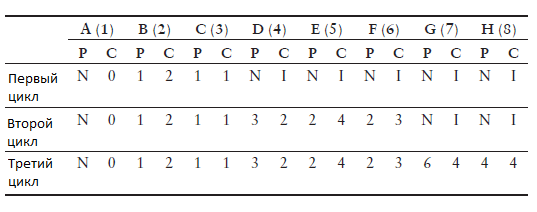
В таблице 2 верхняя строка представляет запись в таблице маршрутизации и узел, доступный в сети. Например, A (1) представляет лучший путь к A, B (2) представляет лучший путь к B и т. д. Столбец P представляет предшественника или узел, через который A должен пройти, чтобы достичь указанного пункта назначения. C представляет собой стоимость достижения этого пункта назначения. Рассмотренный пример сети может быть завершен за три цикла, если алгоритм настроен так, чтобы обнаруживать завершение дерева. Псевдокод, как показано, не имеет никакого теста для этого завершения и в любом случае будет выполнять полные 8 циклов (по одному для каждого узла).
Теперь почитайте про алгоритм диффузного обновления DUAL.
Получите бесплатные уроки на наших курсах
- Data Science с нуля
- Go-программист с нуля
- Фронтенд с нуля
- Python с нуля
- RabbitMQ для разработчиков и DevOps



