Крайне важно осваивать различные методики программирования, которые можно применять для решение огромного количества вычислительных задач, не только для того, чтобы преуспевать на текущей работе, но и иметь возможность получить новую должность в компании вашей мечты.

7 важнейших шаблонов с LeetCode для подготовки к техническому собеседованию
Некоторые разработчики каждый раз заново тратят свое время и силы на поиск нового решения для той или иной задачи. Но при этом вы можете сэкономить время, быстро подобрав эффективное и надежное решение из числа уже существующих методик.
Грамотная подготовка и акцент на навыках решения задач и шаблонах проектирования, которые лежат в их основе, будут иметь решающее значение на конкурсном собеседовании, будь то в компаниях группы FAANG (Facebook, Amazon, Apple, Netflix, Google) или в каких-то других.
LeetCode зарекомендовал себя в качестве отличного ресурса и репозитория для отработки большого количества вопросов, с которыми вы можете столкнуться на технических собеседованиях. Такого рода упражнения необходимы тем, кто готовить проходить собеседование. Но если при этом игнорировать шаблоны, которые относятся к каждому вопросу и ответу, все усилия будут напрасны, поскольку стоит учитывать, что область вычислительной техники довольно широка.
В этой статье мы рассмотрим несколько самых популярных шаблонов, с которыми вы можете столкнуться на технических собеседованиях, чтобы помочь вам подготовиться к нему с помощью LeetCode. Наш структурированный и слаженный подход позволит вам лучше понять общие концепции и шаблоны, которые вы будете использовать.
Давайте приступим!
Что такое LeetCode?
LeetCode – это веб-сайт, который предназначен для обучающихся, чтобы те могли попрактиковаться в решении вычислительных задач, которые часто встречаются на технических собеседованиях. LeetCode содержит более 2 000 задач для тренировки, которые охватывают самые разные концепции и большой список языков программирования. Каждая задача программирования имеет шкалу сложности – Easy (Легко), Medium (Средне) и Hard (Сложно). Все задачи делают упор на структуры данных и алгоритмы.
Ниже приведены несколько примеров задач, которые вы можете там найти:
- Two sum problem (Задача о двух суммах)
- Sorting arrays (Сортировка массивов)
- Largest common subsequences (Наибольшие общие последовательности)
- Valid parentheses (Правильные скобки)
- Search 2D matrix (Поиск двумерной матрицы)
- Valid anagrams (Подходящие анаграммы)
- Binary Search Tree (BST) (Двоичное дерево поиска)
- Level order traversal (Обход по уровням)
- Linked lists (Связные списки)
- Longest substring without repeating characters (Самая длинная подстрока без повторяющихся символов)
- Valid palindromes (Истинные палиндромы)
- Path sum (Сумма путей)
Распознавание шаблонов в методиках и структурах
Вместо того, чтобы ежедневно ломать голову над сотнями слабо связанных между собой задач для технического собеседования, попробуйте решать наборы задач, в которых используется одна и та же структура данных и/или которые решаются с помощью одних и тех же алгоритмических методов. Преуспеете вы с LeetCode или нет зависит не от количества решенных вами задач перед собеседованием, а, скорее, от изучения структур данных и методов их решения. Когда вы познакомитесь с шаблонами, вы сможете применять эти знания для решения большого числа смежных задач, а не только того небольшого числа, с которым вы сталкнетесь на LeetCode.
Перефразируя, шаблоны проектирования кода – это способ установить связь между неизвестной для вас задачей и известной. Давайте рассмотрим некоторые основные шаблоны и то, как их можно использовать на практике.
Метод двух указателей
Когда вы решаете задачи с отсортированными массивами, которые требуют выполнения определенных условий с определенным набором элементов, вам может помочь метод двух указателей. Под набором элементов может пониматься пара, тройка или даже целый подмассив.
Давайте посмотрим на пример такой задачи:
Дан массив отсортированных чисел и целевая сумма. Найдите в массиве пару чисел, сумма которых будет равна целевой.
Самый простой подход к решению данной задачи заключается в том, что мы создаем два вложенных цикла и проверяем все возможные пары чисел с целью найти ту самую пару, чья сумма будет равна целевой. Каждый вложенный цикл будет проходить по всей длине массива. Следовательно, временная сложность такого алгоритма составит O(N2), где N – это количество элементов во входном массиве. Вы могли бы сделать это куда эффективнее с помощью метода двух указателей. Предположим, что входной массив отсортирован, начиная с первого указателя в начале массива и заканчивая вторым указателем в конце массива.
На каждом шаге вы будете видеть, составляют ли числа, на которые указывают эти два указателя, целевую сумму. Если это так, что вы возвращаете два значения, на которые указывают эти указатели. В противном случае вы выполняете одно из следующих двух действий:
- Если сума двух чисел, на которые указывают два указателя, оказалась больше целевой суммы, то это значит, что вам нужна пара чисел, сумма которых будет меньше. Поэтому, чтобы искать дальше, вы должны переместить второй указатель влево.
- Если сумма двух чисел, на которые указывают два указателя, оказалась меньше целевой суммы, то это значит, что вам нужна пара чисел, сумма которых будет больше. Поэтому, чтобы искать дальше, вы должны переместить первый указатель вправо.
Метод двух указателей уменьшает временную сложность решения до ON. Как следствие, такой подход к поиску пары чисел с целевой суммой в массиве является более эффективным.
Метод скользящего окна
Существует большое количество задач, связанных с массивами или связными списками, в которых вас просят найти или вычислить что-то из всех подмассивов заданного размера. Окно – это подсписок, который был сформирован из итерируемой структуры данных. Его можно использовать для перемещения по фрагментам данных, которые соответствуют размеру окна. Так, например, давайте посмотрим на следующую задачу:
Дан массив. Найдите среднее значение каждого подмассива из «К» смежных элементов в нем.
Давайте разберемся с этой задачей на примере:
Массив: [1, 3, 2, 6, -1, 4, 1, 8, 2], K= 5
Здесь вас просят в исходном массиве найти среднее значение всех подмассивов из 5 смежных элементов. Давайте разбираться: для первых 5 чисел (подмассив с 0-го индекса по 4-ый) среднее значение будет 1+3+2+6-1/5=2,2.
Среднее значение следующих пяти чисел (подмассив с 1-го индекса по 5-ый) (3+2+6-1+4)/5=2,8.
Для следующих пяти чисел (подмассив со 2-го индекса по 6-ой) среднее значение (2+6-1+4+1)/5=2,4.
И так далее.
Вот так будет выглядеть окончательный результат, в котором содержатся средние значения всех подмассивов размера 5:
Результат: 2,2;2,8;2,4;3,6;2,8
А теперь давайте рассмотрим два возможных варианта решения для метода скользящего окна.
Метод решения «в лоб»
Вы можете использовать два вложенных цикла: внешний цикл будет перемещаться по окнам, а внутренний будет находить максимум в этом окне. Временная сложность такого подхода в самом наихудшем случае составит ON×K, где N – это количество элементов в массиве, а K – это размер окна.
Сбалансированное двоичное дерево поиска
Лучше всего будет воспользоваться двоичным деревом поиска. Вы начинаете со вставки элементов первого окна в самобалансирующееся двоичное дерево поиска, такое как AVL-дерево. И теперь при каждом перемещении окна мы создаем новое окно, удаляя узел и добавляя в дерево новый. Так как это сбалансированное двоичное дерево поиска, то такие действия, как вставка, удаление и нахождение максимума, имеют временную сложность всего лишь Olog K , где K – это количество элементов в окне. Следовательно, в наихудшем случае задача нахождения максимума в дереве имеет временную сложность ONlog K , где N – это количество элементов в массиве.
Наглядный пример другой задачи со скользящим окном.
Задача о рюкзаке
Этот шаблон основан на хорошо известной одноименной задаче, которая решается с помощью динамического программирования. Вы знаете массу и стоимость каждого из «N» предметов, и вас просят сложить эти предметы в «рюкзак», вместимость которого «С». Цель данной задачи в том, чтобы получить наибольшую прибыль от предметов, сложенных в рюкзак.
Давайте посмотрим на простой пример. Предположим, что владелец магазина хочет перевозить фрукты в рюкзаке таким образом, чтобы он мог получить максимально возможную прибыль от их продажи.
Масса и стоимость фруктов:
Предметы: [Яблоко, Апельсин, Банан, Дыня]
Вес: [2, 3, 1, 4]
Стоимость: [4, 5, 3, 7]
Вместимость рюкзака: 5
Вам нужно постараться поместить в рюкзак различные комбинации фруктов так, чтобы их общий вес не превышал 5. Вот некоторые комбинации:
- Яблоко + Апельсин (общий вес: 5) => стоимость: 9
- Яблоко + Банан (общий вес: 3) => стоимость: 7
- Апельсин + Банан (общий вес: 4) => стоимость: 8
- Банан + Дыня (общий вес: 5) => стоимость: 10
Как вы можете видеть, Банан и Дыня приносят наибольшую прибыль и при этом не превышают максимальный вес.
Итак, если вам дано два целочисленных массива для представления стоимости и массы N предметов, вам необходимо найти подмножество этих предметов, которое бы принесло наибольшую прибыль, но при этом не превысило бы заданное значение С. Каждый предмет можно выбрать только один раз, а значит, он либо может быть выбран, либо пропущен.
Вы можете начать с рекурсивного решения «в лоб», чтобы оценить побочные задачи. После чего поэкспериментируйте с более продвинутыми методами мемоизации и восходящего динамического программирования, чтобы довести шаблон до совершенства.
Ниже приведен пример алгоритма решения «в лоб», который определяет все комбинации набора предметов (A, B, C и D):
для каждого предмета 'i'
создается новый набор, который ВКЛЮЧАЕТ в себя предмет 'i', если общий вес не превышает вместимость, и
происходит рекурсивная обработка оставшегося места в рюкзаке и предметов
создается новый набор БЕЗ предмета 'i', и происходит рекурсивная обработка оставшихся предметов
возвращается набор из двух наборов выше с наибольшей прибылью
Временная сложность такого подхода составляет O2n.
Метод быстрого и медленного указателя
Метод быстрого (fast) и медленного (slow) указателя еще называют «алгоритмом зайца и черепахи». Это алгоритм, в котором используются два указателя, которые перемещаются по массиву, последовательности или связному списку с разной скоростью.
Данный метод, как правило, используют для работы с циклическими связными списками и для поиска цикла в связном списке. Его также называют алгоритмом Флойда - алгоритмом нахождения цикла. Давайте рассмотрим простой пример. Вы создаете два указателя: медленный и быстрый. В каждом наборе элементов медленный указатель перемещается на один шаг, а быстрый – на два.
Это наталкивает нас на две мысли:
Если в связном списке нет цикла, то быстрый указатель дойдет до конца массива быстрее, чем медленный, тем самым доказывая, что цикла нет.
Медленный указатель не сможет догнать быстрый указатель, если в связном списке на самом деле нет цикла. Если связный список все же имеет цикл, то первым в цикл войдет быстрый указатель, а только потом медленный. Оба указателя будут перемещаться по этому циклу бесконечно. Если на каком-то этапе эти указатели встретятся, то вы с уверенностью можете сделать вывод о том, что в связном списке есть цикл. И тут уже дело за вами, смогут ли эти два указателя встретиться.
Когда быстрый указатель приближается сзади к медленному, то есть два варианта развития событий:
- Быстрый указатель отстает от медленного на один шаг.
- Быстрый указатель отстает от медленного на два шага.
Любое другое расстояние между быстрым и медленным указателями рано или поздно сведется к одному из этих двух вариантов.
Давайте рассмотрим эти варианты развития событий с той точки зрения, что быстрый указатель всегда начинает движение первым:
Если быстрый указатель отстает от медленного на один шаг: быстрый указатель перемещается на два шага вперед, а медленный – на один, и они встречаются.
Если быстрый указатель отстает от медленного на два шага: быстрый указатель перемещается на два шага вперед, а медленный – на один. Через какое-то количество шагов получится так, что быстрый указатель будет отставать от медленного на один шаг, что сведет все это к первому варианту. Это значит, что при следующем ходе эти два указателя встретятся.
Получается, что если связный список имеет цикл, то эти два указателя обязательно встретятся.
Временная сложность такого подхода составит On, где n – это общее количество узлов.

Демонстрация работы метода быстрого и медленного указателей на примере связного списка с циклом.
Интервалы слияния
Этот шаблон описывает то, как можно работать с перекрывающимися интервалами. Существует большое количество задач, где вам предстоит столкнуться с поиском или объединением перекрывающихся интервалов. Если у вас есть два интервала («a» и «b»), то существует шесть различных вариантов того, как эти два интервала могут располагаться относительно друг друга.
Ниже на рисунке продемонстрированы все шесть вариантов.

Обязательно ознакомьтесь с этими шестью случаями, они могут помочь вам в решении всех задач, связанных с интервалами.
Вот небольшой пример такой задачи:
Дан список интервалов. Объедините все перекрывающиеся интервалы так, чтобы получился список, состоящий только из взаимоисключающих интервалов.
Интервалы: [[1,4], [2,5], [7,9]]
Результат: [[1,5], [7,9]]
Пояснение: так как два первых интервала [1,4] и [2,5] перекрываются, то мы объединяем их к один интервал [1,5].

Разворот связного списка на месте
На технических собеседованиях нередко участников просят решить задачу, которая заключается в том, что им необходимо поменять связи между набором узлов в связном списке. Вся сложность состоит в том, что это нужно сделать «на месте», то есть только с помощью существующих узлов, не выделяя дополнительную память.
Этот шаблон подробно излагает эффективный способ решения этих противных задач. Давайте рассмотрим пример на С++:
Дан односвязный список. Необходимо развернуть его на месте, то есть без выделения дополнительной памяти.
Решение:
Вы перемещаетесь по связному списку и отслеживаете три узла: текущий, предыдущий и следующий. Отслеживая эти узлы, вы сможете развернуть связный список прямо во время обхода. Если говорить более подробно, то вы должны указать текущий узел на предыдущий. Далее следующий узел становится текущим, и процесс продолжается.
Этот метод имеет пространственную сложнсость O1, и получается, что мы сможет развернуть связный список за один обход. Отсюда, временная сложность этого метода в наихудшем случае составит ON, где N – это количество узлов в связном списке.
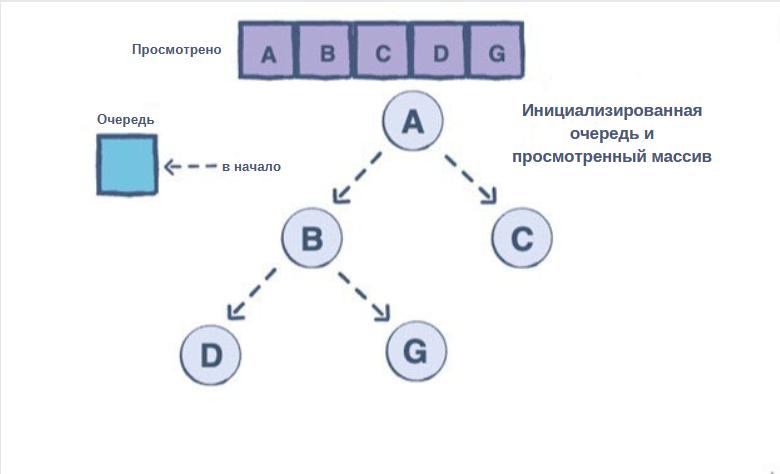
Поиск дерева в ширину
Алгоритм поиска в ширину (BFS – Breadth-first search) применяется для обхода и поиска древовидных или графовых структур данных. Сначала исследуются все узлы текущей глубины, а затем мы переходим к узлам на следующем уровне глубины. Алгоритм BFS, как правило, реализуется с помощью очереди.

С помощью этого подхода можно эффективно решить любую задачу, которая связана с поуровневым обходом дерева. Для отслеживания и рационального обхода всех узлов уровня вам потребуется очередь. Только после того, как вы обойдете один уровень, вы можете перейти к следующему. Это значит, что пространственная сложность алгоритма составит OW, где W – это максимальное количество узлов на каком-либо уровне.
Ниже приведены шаги алгоритма:
- Начинает с того, что добавлчем узел root (корень) в очередь.
- Продолжнаем до тех пор, пока очередь не станет пустой.
- На каждой итерации сначала подсчитываем количество элементов в очереди (давайте назовем его levelSize). Именно столько узлов у нас будет на текущем уровне.
- Затем удаляем узлы, которые мы посчитали в levelSize, из очереди и добавляем их value (значения) в массив для представления текущего уровня.
- Когда мы удаляем узлы из очереди, мы добавляем в нее оба его потомка.
- Если очередь не опустела, то повторяем шаг 3 для следующего уровня.
Продолжайте свою подготовку к собеседованию!
«Дай человеку рыбу, и он будет сыт один день. Научи человека ловить рыбу, и он будет сыт всю жизнь» - довольно известная пословица, которая еще и оказалась актуальной в рамках темы технического собеседования. Не имеет значения сколько рыб вы поймали, если вы не можете повторить этот результат в незнакомом пруду, а все потому, что настоящие профессионалы могут поймать рыбу в любых условиях.
Компании ищут высококвалифицированных разработчиков, которые могут справиться даже с самыми необычными задачами. Именно поэтому ключевым моментов является интенсивная практика этих концепций, потому что, как мы все уже знаем, лучшие разработчики (и рыболовы!) не становятся великими за одну ночь! Решая задачи, связанные с разворотом связных списков или слиянием интервалов, и перемещаясь от задачи к задаче, вы научитесь их решать. А поняв соответствующий базовый принцип, вы приобретете знания и способности, которые помогут вам в решении практически любой задачи, связанной с разворотом связного списка или слиянием интервалов.
Есть еще несколько полезных шаблонов для собеседования, которые мы не рассмотрели здесь подробно:
- K-way merge (k-образный алгоритм слияния)
- Two heaps (Две кучи)
- Cyclic sort (Циклическая сортировка)
- Tree depth-first search (DFS) (Поиск дерева в глубину)
Изучение шаблонов проектирования кода и алгоритмов, лежащих в основе отдельных задач, поможет вам использовать LeetCode и другие источники для подготовки к собеседованию по максимуму!
Получите бесплатные уроки на наших курсах
- Go-программист с нуля
- Data Science с нуля
- Фронтенд с нуля
- RabbitMQ для разработчиков и DevOps
- Python с нуля



