Перед началом убедитесь, что ознакомились с материалом про альтернативные пути без петель.

Частичный и инкрементный SPF
Нет особой причины, по которой весь SPT должен перестраиваться каждый раз, когда происходит изменение топологии сети или информации о доступности. Рассмотрим рисунок ниже для объяснения. Предположим, G теряет связь с 2001: db8: 3e8: 100 :: / 64. Устройству A не требуется пересчитывать свой путь к любому из узлов сети. Доступный пункт назначения - это просто лист дерева, даже если это набор хостов, подключенных к одному проводу (например, Ethernet). Нет причин пересчитывать весь SPT, когда один лист (или любой набор листьев) отключается от сети. В этом случае только лист (IP-адрес Интернет-протокола или доступный пункт назначения) должен быть удален из сети (или, скорее, пункт назначения может быть удален из базы данных без каких-либо изменений в сети). Это частичный пересчет SPT.
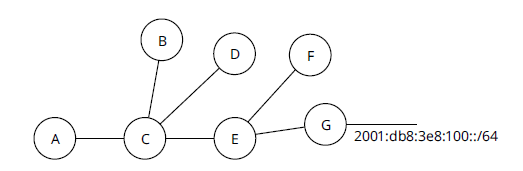
Предположим, что канал [C, E] не работает. Что делает А в этом случае? Опять же, топология C, B и D не изменилась, поэтому у A нет причин пересчитывать все дерево. В этом случае A может удалить все дерево за пределами E. Чтобы вычислить только измененную часть графа, выполните следующие действия:
- Удалите отказавший узел и все узлы, которые нужно достичь через точку E.
- Пересчитайте дерево только от предшественника C (в данном случае A), чтобы определить, есть ли альтернативные пути для достижения узлов, ранее доступных через E до того, как канал [C, E] не доступен.
Это называется инкрементным SPF.
Расчет LFA и rLFA.
В предыдущих лекциях (первой части) по теме «Пути одноадресной передачи без петель» рассматривается теория, лежащая в основе LFA и rLFA. Bellman-Ford не вычисляет ни соседей ниже по потоку, ни LFA, и, похоже, не располагает необходимой для этого информацией. DUAL по умолчанию вычисляет нисходящих соседей и использует их во время конвергенции. А как насчет протоколов на основе Дейкстры (и, соответственно, аналогичных алгоритмов SPF)? На рисунке ниже показан простой механизм, который эти протоколы могут использовать для поиска LFA и соседних узлов ниже по потоку.
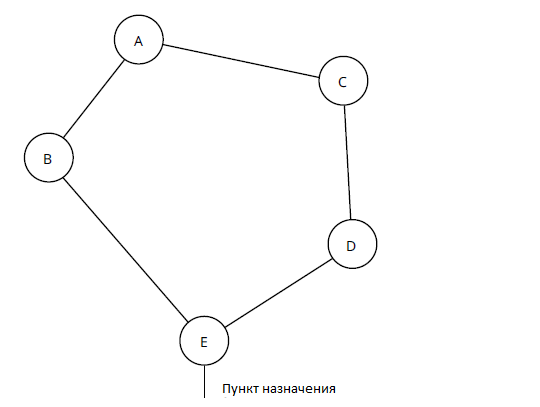
Определение нисходящего соседа - это такое, при котором стоимость достижения соседом пункта назначения меньше, чем локальная стоимость достижения пункта назначения. С точки зрения А:
- A знает местную стоимость проезда к месту назначения на основе SPT, созданного с помощью SPF Дейкстры.
- A знает стоимость B и C, чтобы добраться до места назначения, вычитая стоимость каналов [A, B] и [A, C] из рассчитанной на местном уровне стоимости.
Следовательно, A может сравнивать локальную стоимость со стоимостью от каждого соседа, чтобы определить, находится ли какой-либо сосед в нисходящем направлении по отношению к любому конкретному месту назначения. Определение LFA:
Если затраты соседа для «меня» плюс затраты соседа на достижение пункта назначения ниже, чем местные затраты, соседом является LFA.
Вернее, учитывая:
- NC - это стоимость соседа до пункта назначения.
- BC - это стоимость соседа для меня.
- LC - местная стоимость до места назначения.
Если NC + BC < LC, то соседом является LFA. В этом случае A знает стоимость каналов [B, A] и [C, A] с точки зрения соседа (она будет содержаться в таблице топологии, хотя не используется при вычислении SPT с использованием алгоритма Дейкстры). Таким образом, LFA и нисходящие соседи требуют очень небольшой дополнительной работы для расчета, но как насчет удаленных LFA? Модель P/Q Space обеспечивает простейший способ для алгоритмов на основе Дейкстры вычисления соседних узлов и LFA. Рисунок ниже используется для иллюстрации изнутри P/Q Space.
Определение пространства P - это набор узлов, доступных с одного конца защищенного соединения, а определение пространства Q - это набор узлов, достижимых без пересечения защищенного канала. Это должно предложить довольно простой способ вычисления этих двух пространств с помощью Дейкстры:
Рассчитайте SPT с точки зрения устройства, подключенного к одному концу линии связи; удалить линию связи без пересчета SPT. Остальные узлы доступны с этого конца линии.
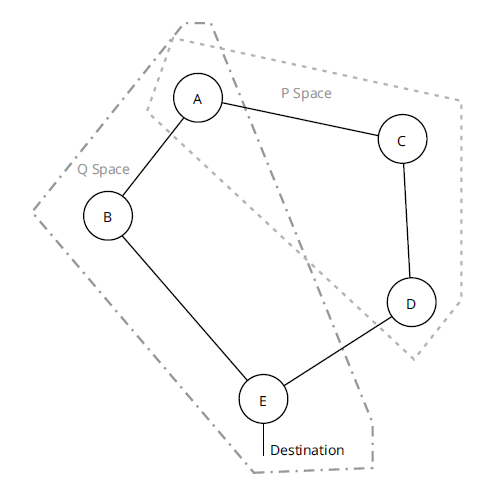
На рисунке E может:
- Вычислите пространство Q, удалив линию [E, D] из копии локального SPT и всех узлов, для достижения которых E использует D.
- Вычислите пространство P, вычислив SPT с точки зрения D (используя D в качестве корня дерева), удалив линию [D, E], а затем все узлы, для достижения которых D использует E.
- Найдите ближайший узел, достижимый как из E, так и из D, с удаленной линией [E, D].
SPF Дейкстры - это универсальный, широко используемый алгоритм для вычисления Shortest Path Trees через сеть.



