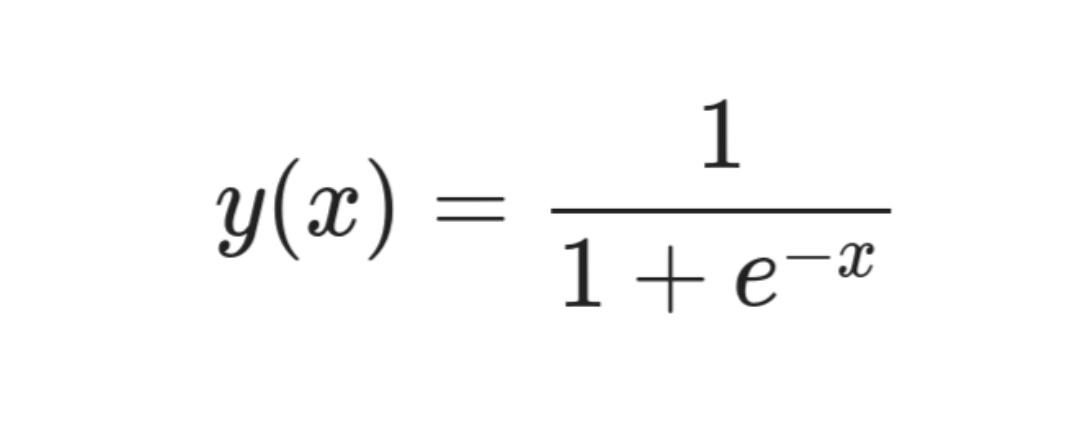В этой статье мы заглянем под капот нейронных сетей и узнаем, как построить её с нуля.

Как построить нейронную сеть с нуля с помощью PyTorch
Как работает нейронная сеть?
Для начала давайте разберемся, как устроены нейронные сети на самом высоком уровне. Нейронная сеть получает набор данных и выдает предсказание. Это очень просто.
Разберем пример. Допустим, один из ваших друзей (который не является большим поклонником футбола) показывает на старую фотографию известного футболиста — скажем, Лионеля Месси — и спрашивает вас о нем.
Вы сможете опознать футболиста за секунду, даже если фотография старая или сделана при тусклом свете. Причина в том, что вы уже тысячу раз видели его фотографии.
Но что произойдет, если вам дадут фотографию известного бейсболиста (а вы никогда раньше не видели ни одного бейсбольного матча)? Вы не сможете узнать этого игрока, даже если фотография будет четкой и яркой.
Этот же принцип используется для нейронных сетей. Если наша цель — создать нейронную сеть для распознавания кошек и собак, мы просто покажем нейронной сети кучу фотографий собак и кошек. Точнее, мы показываем нейросети фотографии собак, а затем говорим ей, что это собаки. А затем показываем ей фотографии кошек и определяем, что это кошки.
Как только мы обучим нашу нейросеть изображениям кошек и собак, она сможет легко классифицировать, кто изображен на картинке - кошка или собака. Короче говоря, она может отличить кошку от собаки.
Но если показать нашей нейросети изображение лошади или орла, она никогда не определит, что это - лошадь или орел. Это происходит потому, что нейросеть никогда не видела изображения лошади или орла, потому что мы никогда не показывали ей этих животных.
Если вы хотите улучшить возможности нейронной сети, вам нужно показать ей фотографии всех животных, которых вы хотите, чтобы нейронная сеть классифицировала. На данный момент она знает только кошек и собак и больше ничего.
Набор данных, который мы используем для обучения, во многом зависит от поставленной перед нами задачи. Если вы хотите определить, положительно или отрицательно настроен твит, то, вероятно, вам понадобится набор данных, содержащий множество твитов с соответствующими метками - положительными или отрицательными.
Теперь, когда у вас есть общее представление о наборах данных и о том, как нейронная сеть обучается на этих данных, давайте углубимся в то, как работают нейронные сети.
Понимание нейронных сетей
Мы будем строить нейронную сеть для классификации цифр три и семь на изображении. Но прежде чем мы построим нейронную сеть, нам нужно глубже понять, как она работает.
Каждое изображение, которое мы передаем нашей нейронной сети, - это просто набор чисел. То есть каждое изображение имеет размер 28×28, что означает, что в нем 28 строк и 28 столбцов, как в матрице.
Мы видим каждую из цифр как полноценное изображение, но для нейросети это просто набор чисел в диапазоне от 0 до 255.
Вот пиксельное представление цифры пять:
Как вы можете видеть выше, у нас 28 строк и 28 столбцов (индекс начинается с 0 и заканчивается на 27), как и в матрице. Нейронные сети видят только эти матрицы 28×28.
Чтобы показать больше деталей, тени идут вместе со значениями пикселей. Если присмотреться к изображению, то можно увидеть, что значения пикселей, близкие к 255, темнее, а значения, близкие к 0, светлее по оттенку.
В PyTorch мы не используем термин матрица. Вместо этого мы используем термин тензор. Каждое число в PyTorch представлено в виде тензора. Поэтому с этого момента мы будем использовать термин тензор вместо матрицы.
Визуализация нейронной сети
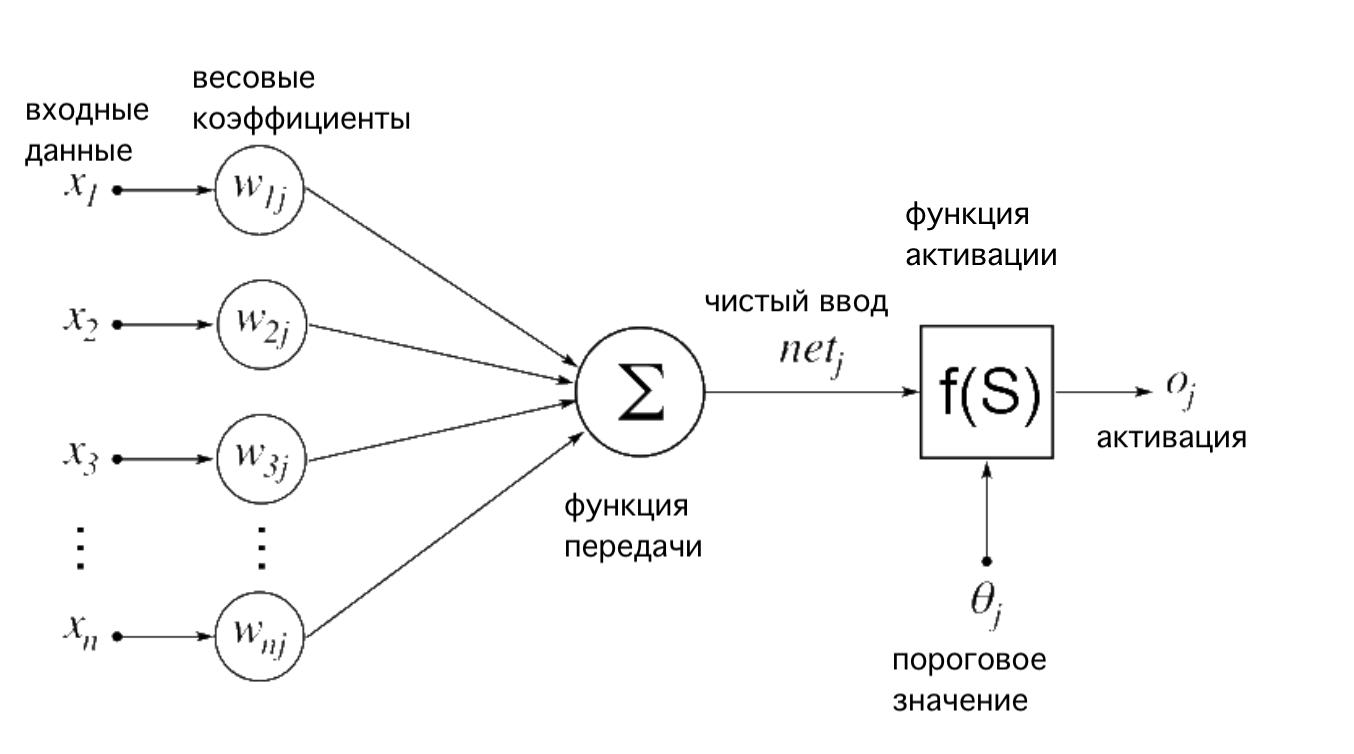
Нейронная сеть может иметь любое количество нейронов и слоев. Вот как выглядит нейронная сеть:
Пусть вас не смущают греческие буквы на картинке.
Возьмем случай, когда нужно предсказать, выживет пациент или нет, на основе набора данных, содержащего имя пациента, температуру, кровяное давление, состояние сердца, месячную зарплату и возраст.
В нашем наборе данных только температура, кровяное давление, состояние сердца и возраст имеют существенное значение для предсказания того, выживет пациент или нет. Поэтому мы присвоим этим значениям больший вес, чтобы показать их большую важность.
Но такие характеристики, как имя пациента и ежемесячная зарплата, практически не влияют на выживаемость пациента. Поэтому мы присваиваем этим признакам меньшие значения веса, чтобы показать их меньшую важность.
На рисунке выше x1, x2, x3...xn - это признаки в нашем наборе данных, которые могут быть значениями пикселей в случае данных об изображениях или такими признаками, как кровяное давление или состояние сердца, как в приведенном выше примере.
Значения признаков умножаются на соответствующие весовые коэффициенты, обозначаемые как w1j, w2j, w3j...wnj. Перемноженные значения суммируются и передаются на следующий слой.
Оптимальные весовые значения узнаются в процессе обучения нейронной сети. Значения весов постоянно обновляются таким образом, чтобы максимизировать количество правильных предсказаний.
Функция активации — это не что иное, как сигмоидная функция в нашем случае. Любое значение, которое мы передаем сигмоиду, преобразуется в значение между 0 и 1. Мы просто накладываем сигмоидную функцию на предсказание нашей нейронной сети, чтобы получить значение между 0 и 1.
Вы поймете важность сигмоидального слоя, когда мы начнем строить нашу модель нейронной сети.
Существует множество других функций активации, которые даже проще в изучении, чем сигмоида.
Это уравнение для сигмоидальной функции:
Узлы круглой формы на диаграмме называются нейронами. На каждом слое нейронной сети веса перемножаются с входными данными. Мы можем увеличить глубину нейронной сети, увеличив количество слоев. Мы можем повысить производительность слоя, увеличив количество нейронов в нем.
Понимание набора данных
Первое, что нам нужно для обучения нашей нейронной сети, это набор данных.
Поскольку цель нашей нейронной сети - классифицировать, содержит ли изображение число три или семь, нам нужно обучить нашу нейронную сеть на изображениях троек и семерок. Итак, давайте создадим наш набор данных.
К счастью, нам не придется создавать набор данных с нуля. Наш набор данных уже присутствует в PyTorch. Все, что нам нужно сделать, — это загрузить его и проделать с ним несколько базовых операций.
Нам нужно загрузить набор данных под названием MNIST (Измененный Национальный институт стандартов и технологий) из библиотеки torchvision в PyTorch.
Что такое набор данных MNIST?
Набор данных MNIST содержит рукописные цифры от 0 до 200 с соответствующими метками, как показано ниже:
Итак, мы просто передаем нейронной сети изображения цифр и соответствующие им метки, которые говорят нейронной сети, что это тройка или семерка.
Как подготовить наш набор данных
В загруженном наборе данных MNIST есть изображения и соответствующие им метки.
Мы просто напишем код, который будет индексировать только изображения с меткой три или семь. Таким образом, мы получим набор данных из троек и семерок.
Сначала импортируем все необходимые библиотеки.
|
import torch from torchvision import datasets import matplotlib.pyplot as plt |
Мы импортируем библиотеку PyTorch для построения нашей нейронной сети и библиотеку torchvision для загрузки набора данных MNIST, как обсуждалось ранее. Библиотека Matplotlib используется для отображения изображений из нашего набора данных.
Теперь давайте подготовим наш набор данных.
|
mnist = datasets.MNIST('./data', download=True) threes = mnist.data[(mnist.targets == 3)]/255.0 sevens = mnist.data[(mnist.targets == 7)]/255.0 len(threes), len(sevens) |
Как мы узнали выше, в PyTorch все представлено в виде тензоров. Поэтому наш набор данных также представлен в виде тензоров.
Мы загружаем набор данных в первой строке. Мы индексируем только те изображения, целевое значение которых равно 3 или 7, нормализуем их путем деления на 255 и сохраняем отдельно.
Мы можем проверить, правильно ли мы проиндексировали, выполнив код в последней строке, который выдает количество изображений в тензоре троек и семерок.
Теперь давайте проверим, правильно ли мы подготовили наш набор данных.
|
def show_image(img): plt.imshow(img) plt.xticks([]) plt.yticks([]) plt.show() show_image(threes[3]) show_image(sevens[8]) |
Используя библиотеку Matplotlib, мы создадим функцию для вывода изображений. Давайте проведем быструю проверку на вменяемость, распечатав форму наших тензоров.
print(threes.shape, sevens.shape) |
Если все прошло правильно, вы получите размеры троек и семерок как ([6131, 28, 28]) и ([6265, 28, 28]) соответственно. Это означает, что у нас есть 6131 изображение размером 28×28 для троек и 6265 изображений размером 28×28 для семерок.
Мы создали два тензора с изображениями троек и семерок. Теперь нам нужно объединить их в один набор данных, который будет использоваться в нашей нейронной сети.
|
combined_data = torch.cat([threes, sevens]) combined_data.shape |
Мы объединим два тензора с помощью PyTorch и проверим форму объединенного набора данных.
Теперь мы сплющим изображения в наборе данных.
|
flat_imgs = combined_data.view((-1, 28*28)) flat_imgs.shape |
Мы сплющим изображения таким образом, чтобы каждое из изображений размером 28×28 стало одной строкой с 784 столбцами (28×28=784). Таким образом, форма преобразуется в ([12396, 784]).
Нам нужно создать метки, соответствующие изображениям в объединенном наборе данных.
|
target = torch.tensor([1]*len(threes)+[2]*len(sevens)) target.shape |
Изображениям, содержащим тройку, мы присваиваем метку 1, а изображениям, содержащим семерку, — метку 0.
Как обучить нейронную сеть
Чтобы обучить нейронную сеть, выполните следующие шаги.
Шаг 1: Построение модели
Ниже приведено простейшее уравнение, которое показывает, как работают нейронные сети:
y = Wx + b
Здесь термин «y» означает наше предсказание, то есть три или семь. 'W' - это значения весов, 'x' - входное изображение, а 'b' - смещение (которое, наряду с весами, помогает делать прогнозы).
Короче говоря, мы умножаем значение каждого пикселя на значения весов и прибавляем их к значению смещения.
Веса и величина смещения определяют важность каждого значения пикселя при составлении прогноза.
Мы классифицируем три и семь, поэтому у нас есть только два класса для предсказания.
Поэтому мы можем предсказать 1, если изображение равно трем, и 0, если изображение равно семи. Предсказание, которое мы получим в результате этого шага, может быть любым реальным числом, но нам нужно, чтобы наша модель (нейронная сеть) предсказывала значение между 0 и 1.
Это позволяет нам создать порог в 0,5. То есть если предсказанное значение меньше 0,5, то это семерка. В противном случае это тройка.
Для получения значения между 0 и 1 мы используем сигмоидальную функцию.
Мы создадим функцию сигмоида, используя то же уравнение, которое было показано ранее. Затем мы передадим в сигмоид значения из нейронной сети.
Мы создадим однослойную нейронную сеть.
Мы не можем создавать много циклов для умножения каждого значения веса на каждый пиксель изображения, так как это очень дорого. Поэтому мы можем использовать магический трюк, чтобы выполнить все перемножение за один раз, используя матричное умножение.
|
def sigmoid(x): return 1/(1+torch.exp(-x)) def simple_nn(data, weights, bias): return sigmoid((data@weights) + bias) |
Шаг 2: Определение потерь
Теперь нам нужна функция потерь, чтобы вычислить, на сколько наше предсказанное значение отличается от истинного.
Например, если предсказанное значение равно 0,3, а истинное - 1, то наши потери очень велики. Поэтому наша модель будет пытаться уменьшить этот убыток, обновляя веса и смещение таким образом, чтобы наши предсказания стали близки к истине.
Для проверки величины потерь мы будем использовать среднюю квадратичную ошибку. Среднеквадратичная ошибка - это среднее квадратическое значение разницы между предсказанным значением и истинным значением.
def error(pred, target): return ((pred-target)**2).mean() |
Шаг 3: Инициализация значений весов
Мы просто произвольно инициализируем веса и смещение. Позже мы увидим, как эти значения обновляются для получения наилучших предсказаний.
|
w = torch.randn((flat_imgs.shape[1], 1), requires_grad=True) b = torch.randn((1, 1), requires_grad=True) |
Форма значений весов должна иметь следующий вид:
(количество нейронов в предыдущем слое, количество нейронов в следующем слое).
Мы используем метод градиентного спуска для обновления весов и смещения, чтобы сделать максимальное количество правильных предсказаний.
Наша цель — оптимизировать или уменьшить потери, поэтому лучший метод - вычисление градиентов.
Нам нужно взять производную каждого веса и смещения по отношению к функции потерь. Затем мы должны вычесть это значение из наших весов и смещений.
Таким образом, значения весов и смещения обновляются так, чтобы наша модель делала хорошие предсказания.
Обновление параметра для оптимизации функции не является чем-то новым - вы можете оптимизировать любую произвольную функцию с помощью градиентов.
Мы установили специальный параметр (называется requires_grad) в true, чтобы вычислить градиент весов и смещения.
Шаг 4: Обновление весов
Если наше предсказание не совпадает с истинным, это означает, что мы сделали неправильное предсказание. Это означает, что наши веса не верны. Поэтому нам нужно обновлять веса до тех пор, пока мы не получим хорошие предсказания.
Для этого мы помещаем все описанные выше шаги в цикл for и позволяем ему повторяться любое количество раз.
На каждой итерации вычисляется потеря и обновляются веса и смещения, чтобы получить лучший прогноз на следующей итерации.
Таким образом, наша модель становится лучше после каждой итерации, находя оптимальное значение веса, подходящее для конкретной задачи.
Для каждой задачи требуется свой набор значений весов, поэтому мы не можем ожидать, что нейронная сеть, обученная классифицировать животных, будет хорошо справляться с классификацией музыкальных инструментов.
Вот как выглядит обучение нашей модели:
|
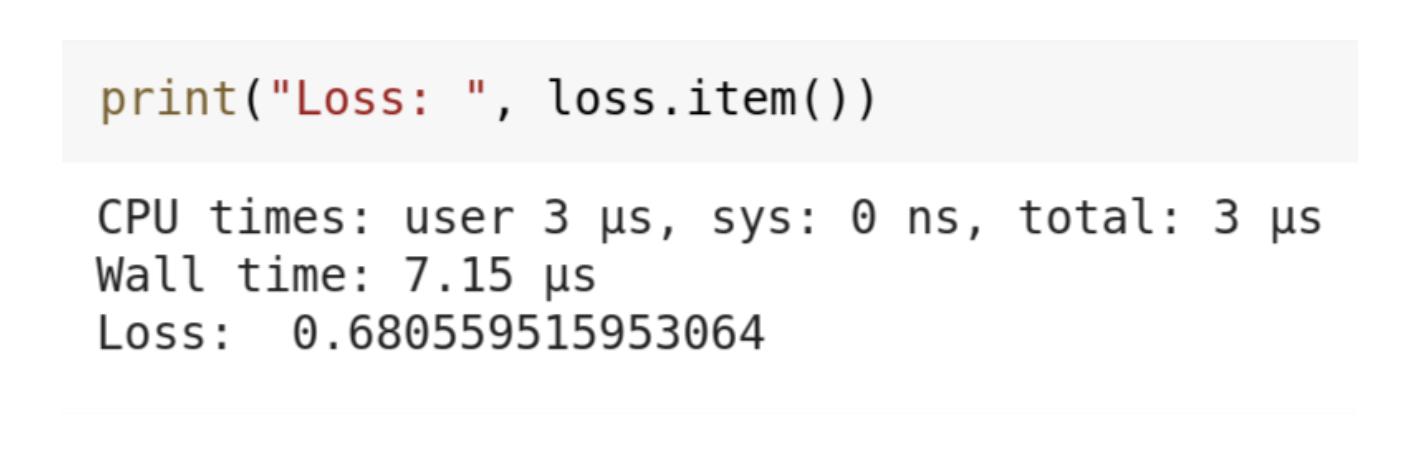
for i in range(2000): pred = simple_nn(flat_imgs, w, b) loss = error(pred, target.unsqueeze(1)) loss.backward() w.data -= 0.001*w.grad.data b.data -= 0.001*b.grad.data w.grad.zero_() b.grad.zero_() print("Loss: ", loss.item()) |
Мы вычислим предсказания и сохраним их в переменной 'pred', вызвав функцию, которую мы создали ранее. Затем мы рассчитаем среднюю квадратичную ошибку.
Затем мы рассчитаем все градиенты для наших весов и смещения и обновим значение, используя эти градиенты.
Мы умножили градиенты на 0,001, и это называется скоростью обучения. Это значение определяет скорость, с которой будет обучаться наша модель. Если оно слишком мало, то модель будет обучаться медленно, или, другими словами, потери будут уменьшаться медленно.
Если скорость обучения слишком высока, наша модель не будет стабильной, прыгая между широким диапазоном значений потерь. Это означает, что она не сможет сходиться.
Мы проделываем описанные выше шаги 2000 раз, и каждый раз наша модель пытается уменьшить потери, обновляя значения весов и смещения.
Мы должны обнулять градиенты в конце каждого цикла или эпохи, чтобы в памяти не накапливались нежелательные градиенты, которые повлияют на обучение модели.
Поскольку наша модель очень мала, обучение в течение 2000 эпох или итераций не займет много времени. После 2000 эпох наша нейронная сеть дала значение потерь 0,6805, что неплохо для такой маленькой модели.
Подведем итоги
В модели, которую мы только что создали, есть огромное пространство для совершенствования.
Это всего лишь простая модель, и вы можете экспериментировать с ней, увеличивая количество слоев, число нейронов в каждом слое или количество эпох.
Одним словом, машинное обучение - это сплошная магия с использованием математики. Всегда изучайте фундаментальные концепции - они могут быть скучными, но со временем вы поймете, что эти скучные математические концепции создали эти передовые технологии, такие как deepfakes.
Получите бесплатные уроки на наших курсах
- полный курс по Git
- RabbitMQ для разработчиков и DevOps
- Data Science с нуля
- Нейросети с нуля
- Аналитик данных с нуля