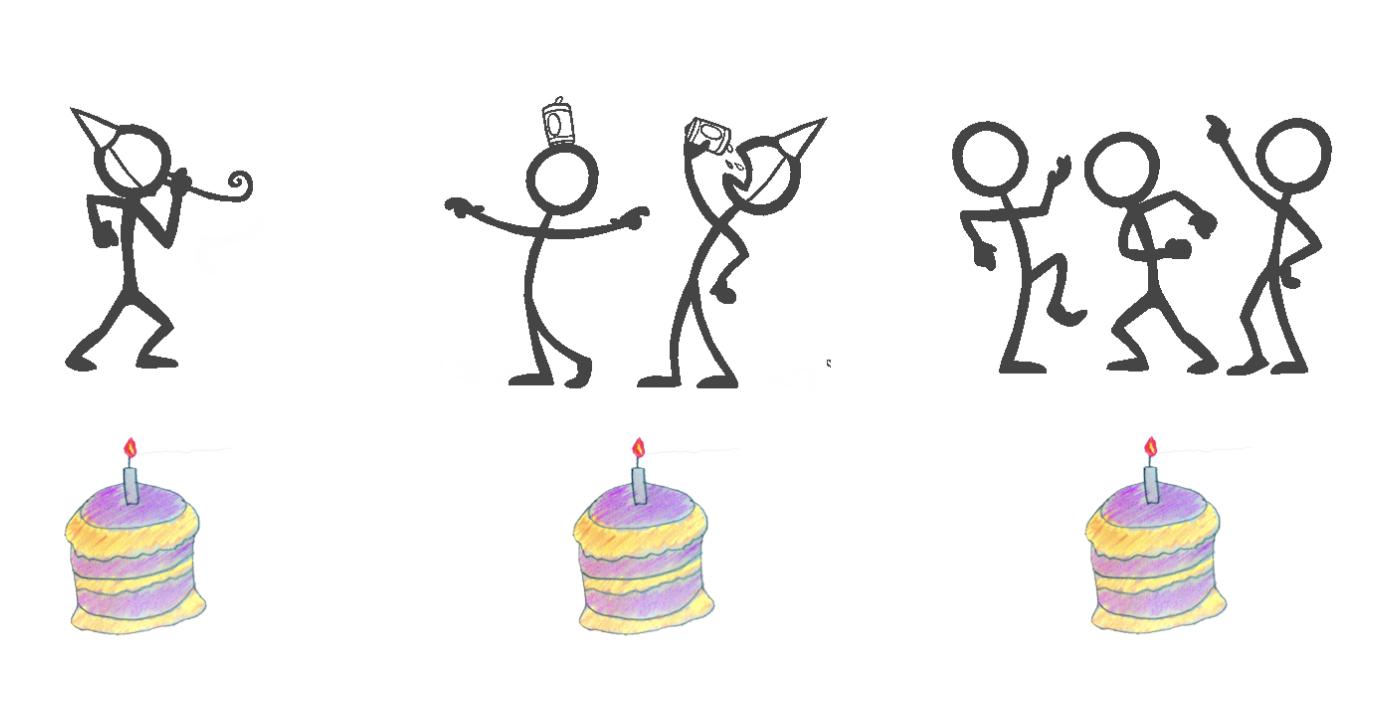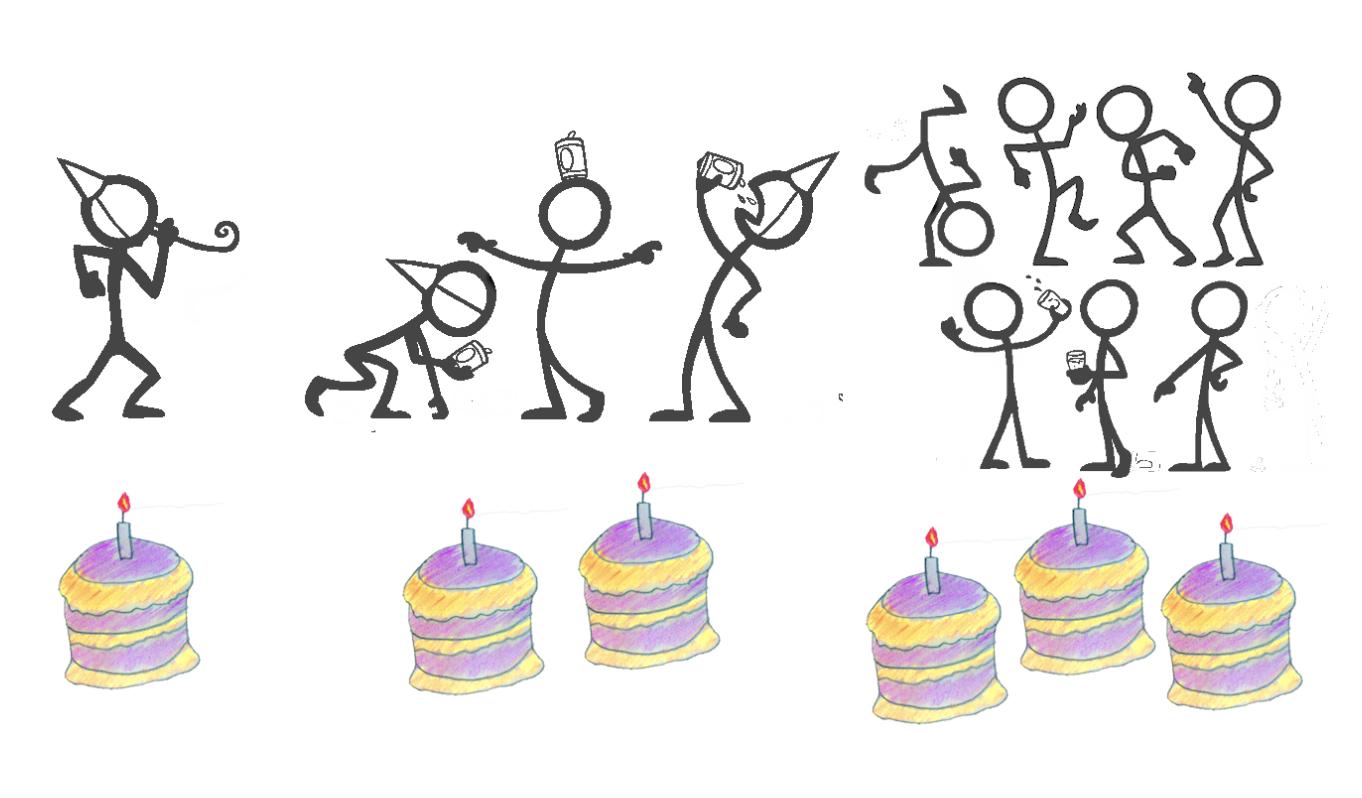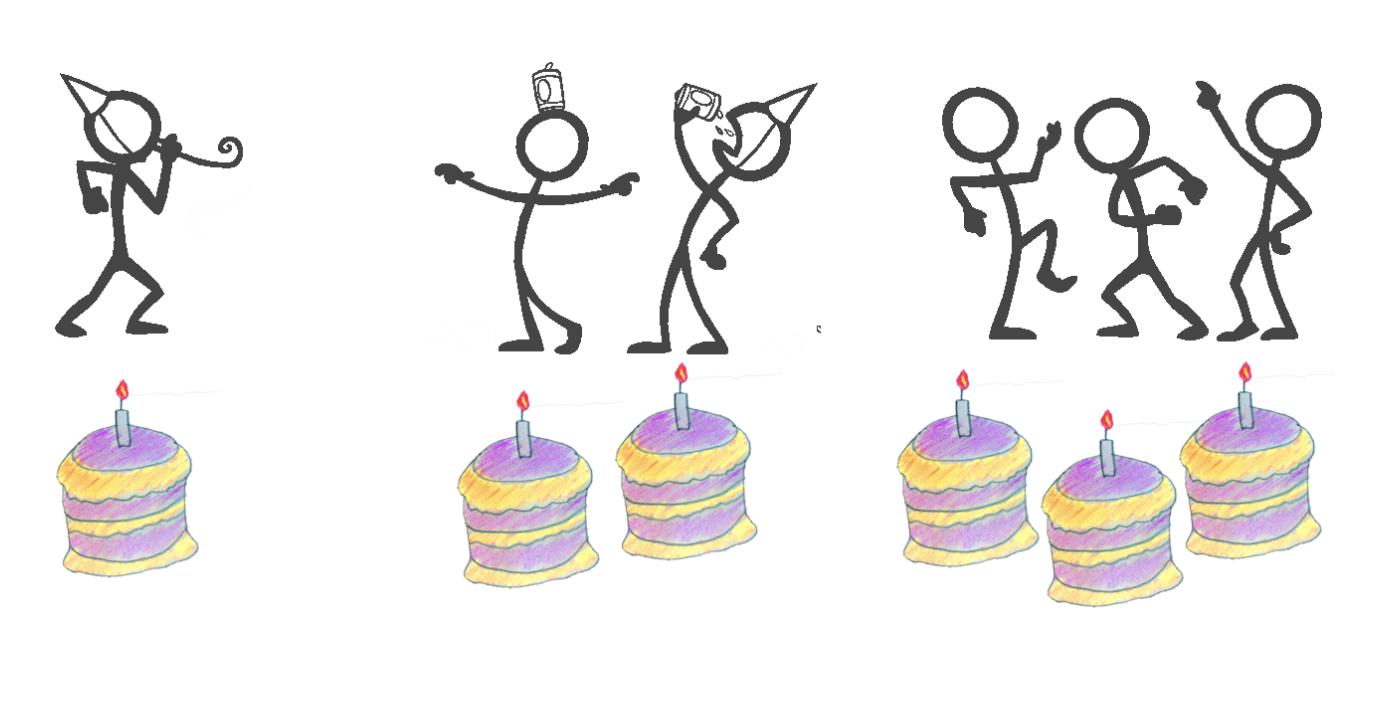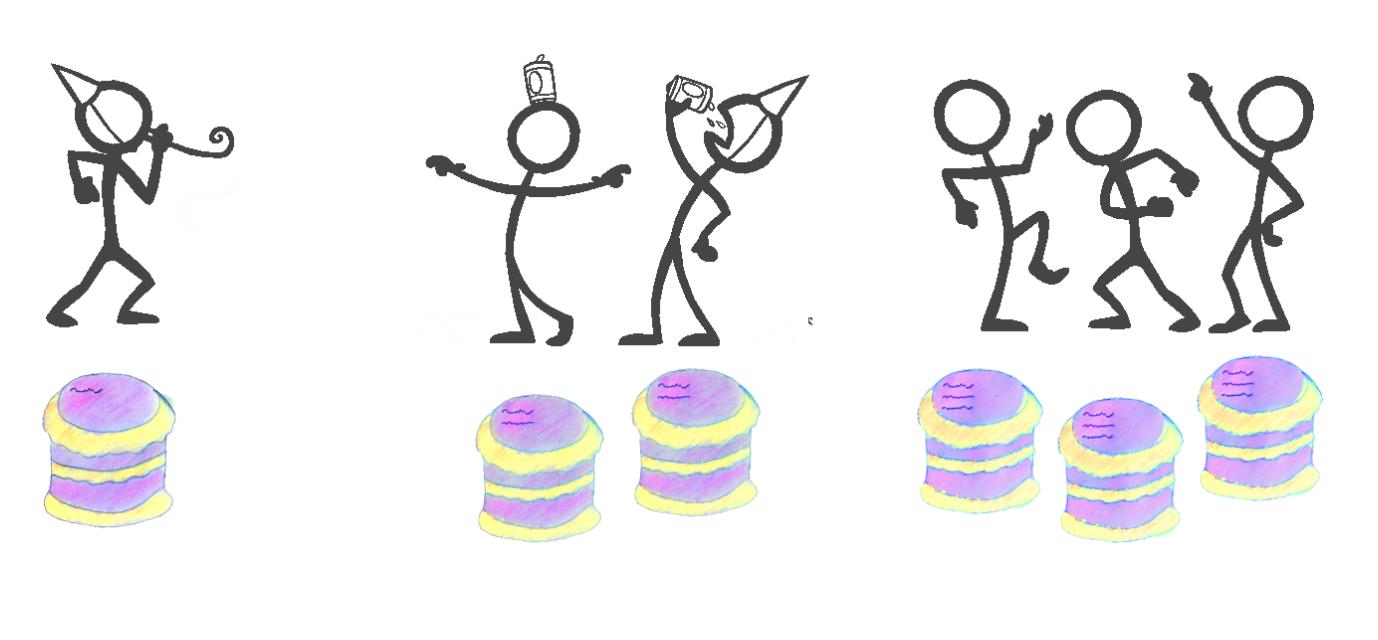Нотация Big O используется в информатике для определения верхней границы алгоритма. В основном она нужна, чтобы рассчитать максимальное время работы алгоритма в зависимости от размера входных данных, но также может применяться для определения объема памяти.

Как работает Big O Notation: разбираем на примере кекса
В этой статье мы рассмотрим наиболее распространенные типы нотации Big O, используя для иллюстрации концепций праздничные торты. Мы представим, что устраиваем вечеринку, и нам нужно определить, сколько тортов нужно испечь в зависимости от количества присутствующих.
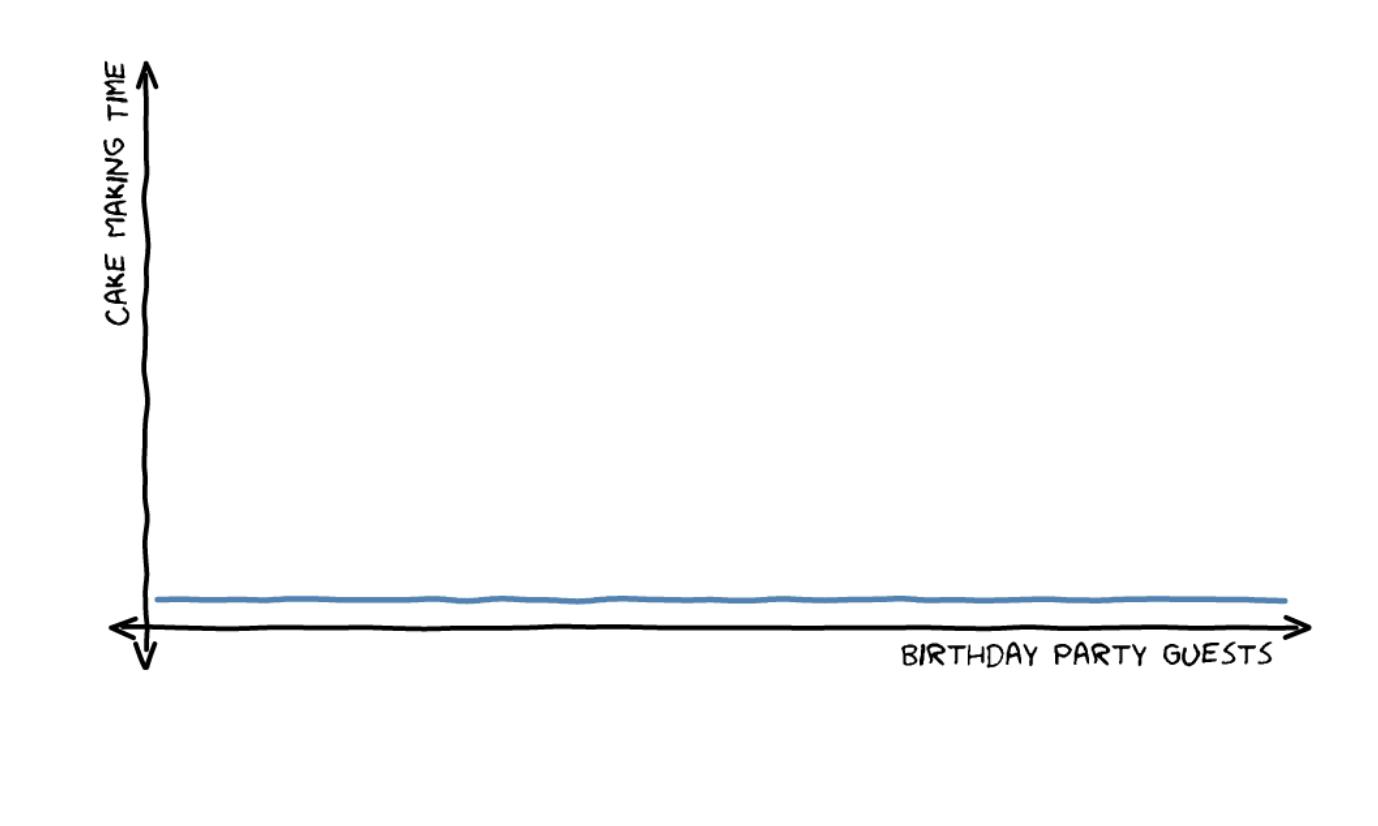
O(1) — постоянное время
В примере с постоянным временем неважно, сколько человек придет на день рождения, вы испечете только один торт. Поэтому время приготовления торта остается постоянным.
Обратите внимание, что в нотации Big O не указывается, сколько длится постоянное время (может быть, на приготовление торта уходит 1 час, а может быть, 4 часа). Она просто указывает, что время, затраченное на это, не увеличивается с ростом числа гостей.
Реальный пример операции O(1) - это обращение к массиву по его индексу. Получить элемент из массива, состоящего из 10 элементов, можно так же быстро, как и из массива, состоящего из 1 миллиона элементов.
O(log n) — логарифмическое время
В примере с логарифмическим временем праздничные торты используются для того, чтобы стимулировать людей приходить на вечеринку вовремя.
Первый пришедший получает торт в свое распоряжение. Затем следующие 2 человека делят между собой торт. Затем следующие 4 человека делят торт и так далее.
Таким образом, для вечеринки на 1 человека требуется 1 торт. Для вечеринки на 2 или 3 человека требуется 2 торта. Для вечеринки на 4 - 7 человек требуется 3 торта, а для вечеринки на 8 - 15 человек - 4 торта. В общем случае для вечеринки на n человек требуется log2(n) тортов.
Наиболее распространенным примером операции O(log n) в реальном мире является бинарный поиск в упорядоченном массиве.
Этот алгоритм просматривает середину массива и смотрит, меньше или больше искомое значение. Поскольку список упорядочен, он узнает, в какой половине массива находится искомое значение.
Затем он повторяет процесс с этой половиной массива. Таким образом, для массива из 16 элементов первая итерация сужает поиск до 8 элементов, затем до 4, затем до 2 и затем до 1, всего 4, или log2(16), итераций.
Наиболее распространенным примером операции O(log n) в реальном мире является бинарный поиск в упорядоченном массиве.
Этот алгоритм просматривает середину массива и смотрит, меньше или больше искомое значение. Поскольку список упорядочен, он узнает, в какой половине массива находится искомое значение.
Затем он повторяет процесс с этой половиной массива. Таким образом, для массива из 16 элементов первая итерация сужает поиск до 8 элементов, затем до 4, затем до 2 и затем до 1, всего 4, или log2(16), итераций.
O(n) — линейное время
В примере с линейным временем каждый гость получает свой торт. Если на вечеринку пришло n человек, вам нужно испечь n тортов. Таким образом, затраченное время зависит от количества гостей.
Опять же, в нотации Big O не указывается, как долго длится процесс (может быть, на приготовление торта уходит 1 час, а может быть, 4 часа), а просто говорится, что время линейно увеличивается с ростом числа гостей.
Реальный пример операции O(n) - это наивный поиск элемента в массиве. В массиве из 10 элементов, в худшем случае, вам придется просмотреть все 10 элементов, чтобы найти тот, который вам нужен. Но для массива из 1 миллиона элементов вам, возможно, придется просмотреть все 1 миллион.
Конечно, вы можете найти решение и быстрее, но обозначение Big O указывает максимальное количество времени, которое займет алгоритм.
O(n^2) — квадратичное время
В примере с квадратичным временем каждый гость получает свой собственный торт. Кроме того, на каждом торте написаны имена всех гостей, а также вкусная глазурь.
В этом случае на вечеринке на 1 человека будет один торт с одним именем. Для вечеринки на 2 человека - два торта, на обоих по два имени (всего 4 имени), а для вечеринки на 3 человека - три торта, на каждом из которых по три имени, то есть всего 9 имен.
В общем случае для вечеринки на n человек требуется написать n*n имен (также известное как n в квадрате, или n в степени 2), поэтому скорость приготовления тортов (и написания всех имен) зависит от квадрата числа гостей.
Реальный пример операции O(n^2) - это наивный поиск дубликатов в массиве. В этом случае вы перебираете все элементы в массиве и для каждого из них снова просматриваете массив на предмет совпадений.
Для массива из 10 элементов внешний цикл имеет 10 итераций, и для каждой из них есть 10 итераций внутреннего цикла, итого 100. Для массива из 1 миллиона элементов - 1000 миллиардов.
Существует более общий случай O(n^2), когда вместо того, чтобы время относилось к n в степени 2 (n^2), оно относится к n в степени c (n^c). Такое время обычно называют полиномиальным.
O(n!) — факториальное время
В примере Factorial Time гости участвуют в соревновании по петанку, и победитель забирает домой торт.
Правда, есть небольшая проблема: игрок, который делает первый ход, оказывается в невыгодном положении. Чтобы выровнять ситуацию, проводится много игр, чтобы все перестановки гостей были охвачены и каждый получил возможность ходить первым. Все эти перестановки написаны на торте, опять же с помощью вкусной глазури.
Это означает, что на вечеринку из двух человек приходится две игры, поскольку каждый гость по очереди ходит первым. На вечеринке из трех человек - 6 игр (если представить, что гости - Анна, Брайан и Крис, то перестановки будут ABC, ACB, BAC, BCA, CAB, CBA).
В общем случае для вечеринки на n человек требуется n!, или n факториалов, поэтому скорость приготовления торта зависит от этого.
n! вычисляется путем умножения всех целых чисел от n до единицы «n (n - 1) (n - 2) ... 2 1». Таким образом, для вечеринки из двух человек это 2 1, или 2. Для партии из трех человек это 3 2 * 1, то есть 6.
Реальные примеры операций O(n!) - это все, что требует анализа списка перестановок, например, задача о путешествующем продавце.
Выводы
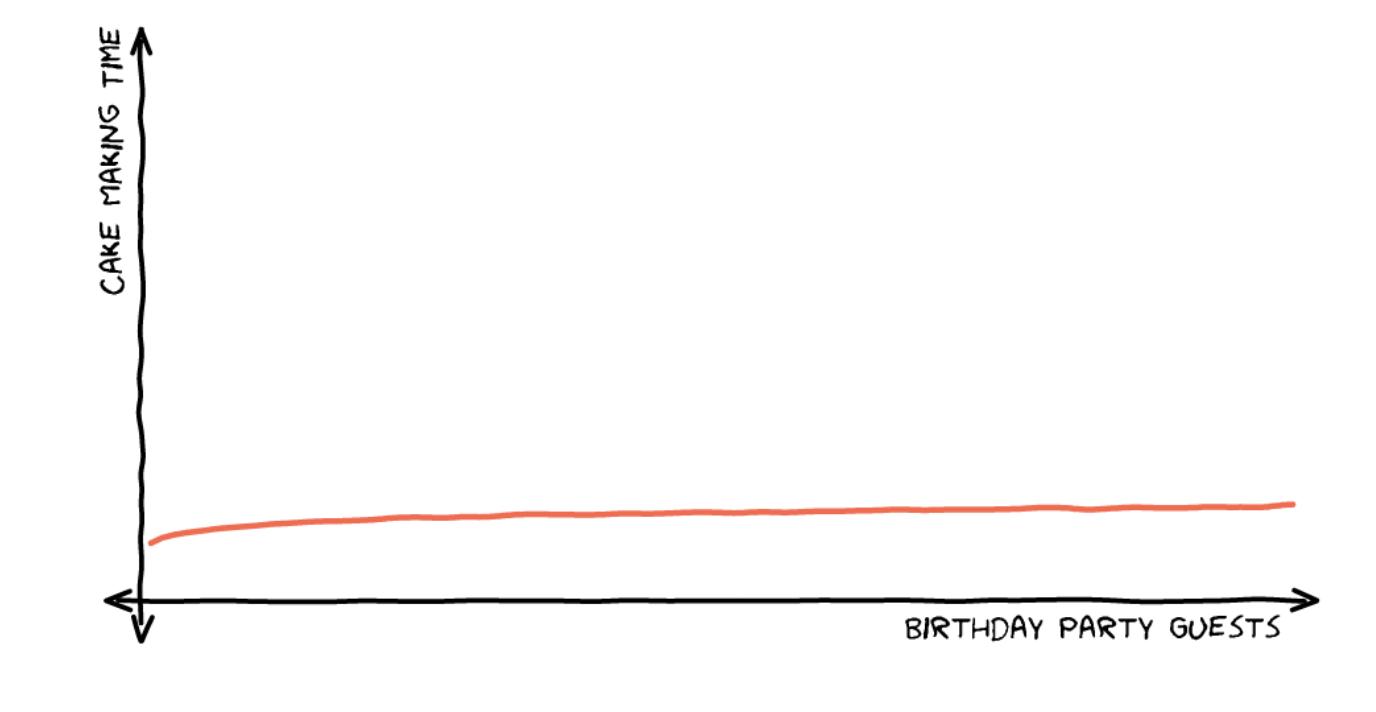
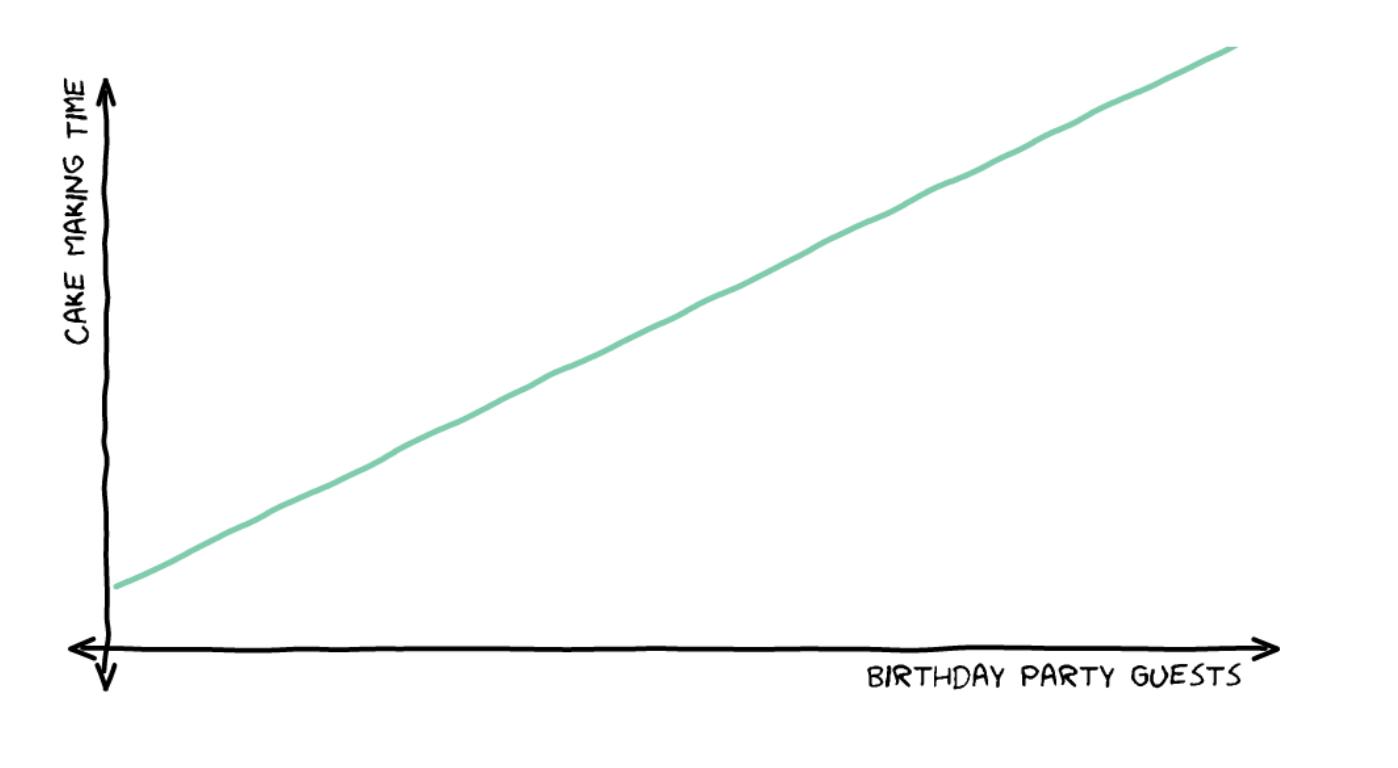
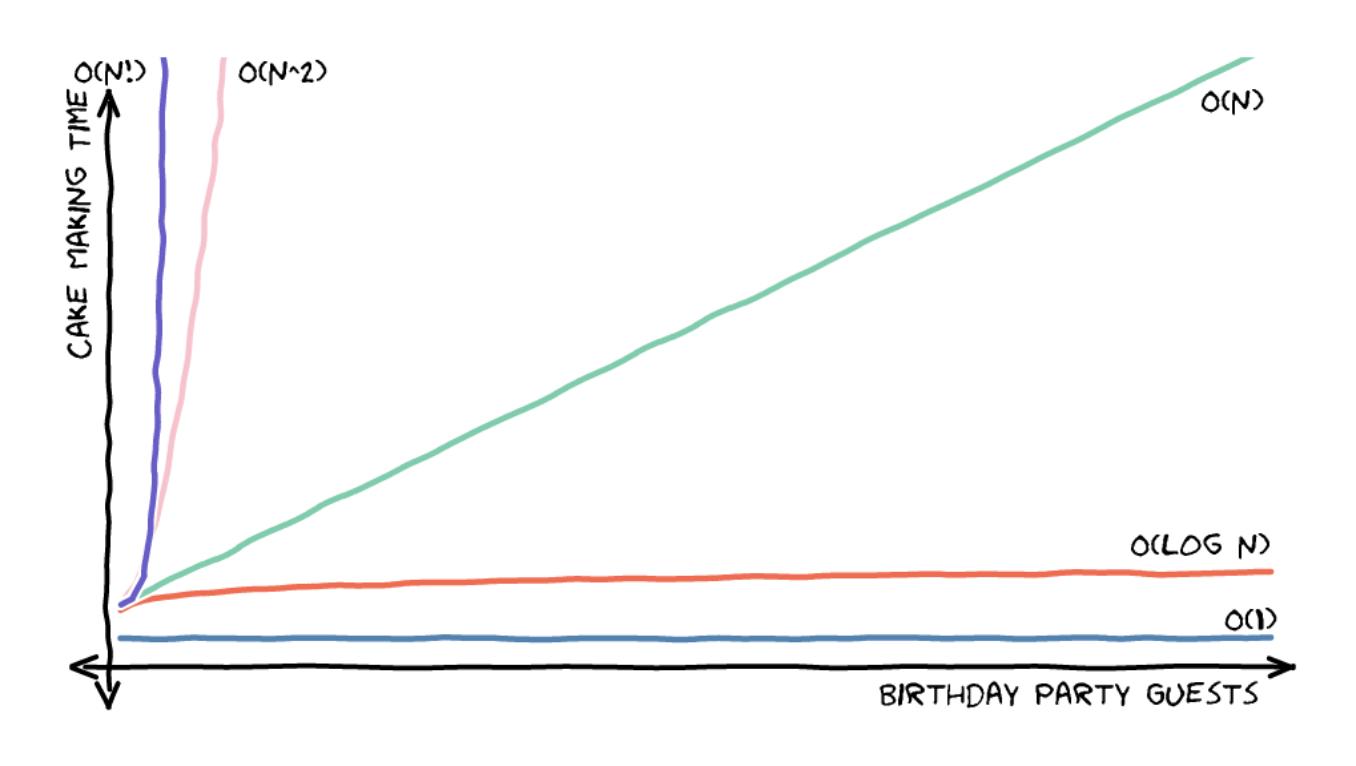
Надеемся, благодаря праздничным тортам нотация Big O стала легче усваиваться! График ниже также хорошо помогает запоминанию, показывая относительную скорость алгоритмов (если есть выбор, то лучше выбрать более быстрый!)