Давайте рассмотрим следующую ситуацию: Санта приносит игрушки всем хорошим девочкам и мальчикам.
На 2019 год в мире проживало 7 713 468 100 человек, около 26,3% из которых моложе 15 лет. Это 2 028 642 110 детей (лиц в возрасте до 15 лет) в мире.
Есть такое мнение, что Санта посещает детей не всех религий, поэтому мы обобщим и включим в рассмотрение только христиан и нерелигиозных людей. В совокупности это примерно 44,72% населения. Если мы предположим, что дети исповедуют ту же религию, что и родители, то получится, что Санта-Клаус должен посетить 907 208 751,6 детей.
Какой процент из этих детей хорошие? Это узнать невозможно; однако мы можем поработать с несколькими предположениями. Во-первых, Санта-Клаус действует больше из соображений оптимизма, а не экономии, так что, он, вероятно, был бы готов к возможности того, что каждый ребенок будет хорошим в любой год. Таким образом, он был бы готов дать игрушку каждому ребенку. Предположим, что это был отличный год и все 907 208 751,6 детей получили игрушки.
Подарков много, и, как мы знаем, все они сделаны эльфами Санты в его мастерской на Северном полюсе. Учитывая, что в году 365 дней, и один из них – Рождество, то будем считать, что у Санты есть 364 дня, чтобы сделать и упаковать 907 208 752 (округлим) подарка. Получается 2 492 331,74 подарка в день.
Почти два с половиной миллиона подарков в день – большая нагрузка для любой мастерской. Давайте рассмотрим два подхода, которые Санта может использовать, чтобы упаковать все подарки: конкурентное исполнение (конкурентность) и параллельное исполнение (параллелизм).
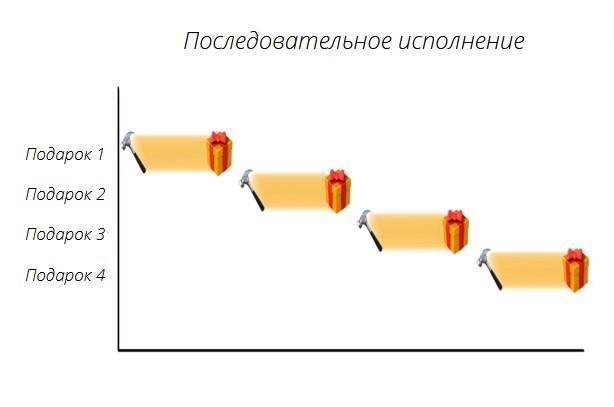
Последовательный процесс
Предположим, что в мастерской Санты-Клауса работает ровно один очень трудолюбивый и очень уставший эльф. Один подарок изготавливается за четыре этапа:
- Раскрой дерева
- Сборка и склейка игрушки
- Роспись игрушки
- Подарочная упаковка
Когда эльф только один, то в любой момент времени он может выполнять лишь один этап для одного подарка. Если бы эльф производил по одному подарку от начала и до конца, то этот процесс был бы последовательным. Но это не самый эффективный способ для того, чтобы изготовить два с половиной миллиона подарков за день. Например, эльфу придется ждать и при этом ничего не делать, пока клей на игрушке не высохнет, и он сможет перейти к следующему этапу.
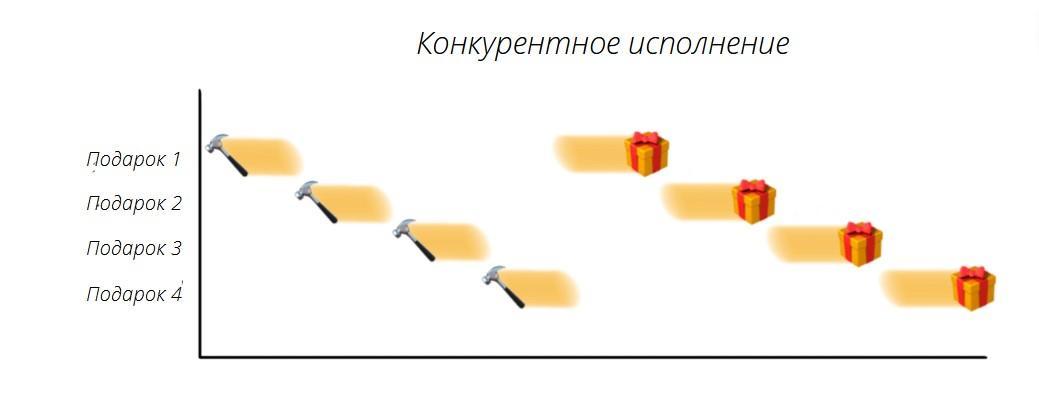
Конкурентность
Для того, чтобы быть более продуктивным, эльф может работать над всеми подарками одновременно.
Вместо того, чтобы делать по одному подарку за раз, эльф сначала раскраивает всю древесину для всех игрушек, одну за другой. Когда все вырезано, эльф собирает и склеивает игрушки одну за другой. При такой одновременной обработки клей на первой игрушке успевает высохнуть (не требуя особого внимания со стороны эльфа), пока склеиваются другие игрушки. То же самое касается росписи и упаковки.
Так как один эльф может выполнять только одну задачу за раз, то, если он будет производить подарки одновременно, он будет использовать день максимально эффективно.
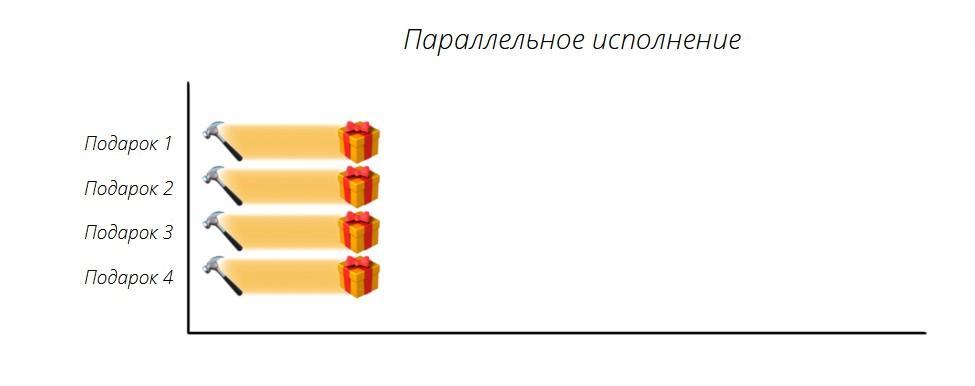
Параллелизм
Хотелось бы надеяться, что в мастерской Санты все же больше, чем один эльф. Чем больше эльфов, тем больше игрушек можно сделать одновременно в течение дня. Такая одновременная работа означает, что подарки производятся параллельно. Параллельная работа нескольких эльфов означает, что одновременно выполняется больше работы.
Эльфы, которые работают параллельно, также могут использовать конкурентность. Один эльф по-прежнему может решать только одну задачу за раз, поэтому самым эффективным вариантом будет иметь несколько эльфов, которые будут производить подарки одновременно.
Конечно, если в мастерской Санты, скажем, два с половиной миллиона эльфов, то тогда каждый эльф должен будет сделать максимум один подарок за день. В таком случае последовательная работа не снижает эффективности. И осталось бы еще 7 668,26 эльфов, которые приносили бы кофе и обед.
Санта-Клаус и многопоточность
После того, как эльфы выполнили всю тяжелую работу, Санта-Клаус должен доставить подарки – все 907 208 752.
Санте не нужно навещать каждого ребенка лично; только елку в доме. Итак, сколько же елок ему нужно посетить? Опять же, обобщая, мы скажем, что среднее количество детей в семье во всем мире составляет 2,45 (будем основываться на прогнозируемых коэффициентов рождаемости на этот год). Получается, что Санта должен посетить 370 289 286,4 дома. Давайте округлим до 370 289 287.
Сколько на это есть времени у Санты? Легенды гласят об одной ночи, что означает один оборот Земли, а, значит, 24 часа. NORAD это подтверждает.
Это значит, что Санта должен посетить 370 289 287 домов за 24 часа (86 400 секунд). Следовательно, его скорость должна составлять 4 285,75 домов в секунду, и мы еще не упоминали о, которое нужно для того, чтобы положить подарки под елку и взять печенье.
Понятно, что Санты в нашем измерении не существует. Хотя бы потому, что он достаточно пухлый и при этом он пролезает в дымоход (с зажженным огнем, оставаясь невредимым) с мешком игрушек для всех детей семьи. И это мы еще не учли тот факт, что его сани везут огромное количество игрушек для каждого верующего ребенка во всем мире и что они летают.
Существует ли Санта вне наших законов физики? Как мог кто-то реальный путешествовать по миру, доставляя посылки менее чем за 24 часа со скоростью 4 285,75 домов в секунду, и при это у него еще оставалось время на молоко, печенье и поцелуй мамочки?
Одно можно сказать наверняка: Санта пользуется Интернетом. Никакая другая технология еще не позволяла посылкам перемещаться так далеко и так быстро. Как бы там ни было, попытка охватить более четырех тысяч домов в секунду – непростая задача, даже имея в арсенале лучшее гигабитное Интернет-соединение, которое может предоставить Северный полюс. Как Санта может повысить свою эффективность?
Очевидно, что у этой загадки есть только один логичный ответ: Санта-Клаус – это многопоточный процесс.
Один поток
Давайте посмотрим на это все со стороны. Представим, что поток – это одна конкретная задача или детализированная последовательность инструкций, которую может выполнить Санта. Один поток может выполнить только одну задачу – положить подарок под елку. Поток – это некий компонент процесса, в данном случае процесса доставки подарков Санта-Клаусом.
Если бы Санта-Клаус был бы однопоточным, то он как любой однопоточный процесс мог бы выполнять лишь одну задачу за раз. Поскольку он стар и у него не такая хорошая память, то у него, вероятно, есть набор инструкций по доставке подарков, а также график, которого стоит придерживаться. Эти две вещи направляют поток Санты, пока его процесс не завершится.
Однопоточный Санта-Клаус работает примерно по следующей схеме:
- Посадить сани у дома Тимми.
- Достать подарок Тимми из саней.
- Войти в дом через дымоход.
- Найти рождественскую елку.
- Положить подарок Тимми под рождественскую елку.
- Выйти из дома через дымоход.
- Взлететь на санях.
И так по кругу… еще 370 289 286 раз.
Многопоточность
Многопоточный Санта-Клаус, напротив, является доктором Манхэттеном Северного полюса. В мире существует все еще один Санта-Клаус, но у него есть удивительная способность размножить свое сознание и одновременно выполнять несколько наборов инструкций. Эти дополнительные рабочие задачи, или рабочие потоки, создаются и контролируются основным процессом доставки подарков Санта-Клауса.
Каждый рабочий поток действует независимо, выполняя свои инструкции. Так как все они являются копией сознания Санты, то у них есть его память, и они знают все, что знает Санта, в том числе то, как устроена планета, по которой они доставляют подарки, и откуда эти подарки брать.
Благодаря этим знаниям каждый поток может выполнять свой набор инструкций параллельно с другими потоками. Такой многопоточный параллелизм делает единственного и неповторимого Санта-Клауса максимально продуктивным.
Если в среднем выполнение доставки подарка занимает час, то Санте нужно создать всего 4 286 рабочих потоков. Совершая по одной доставке в час таким образом, Санта завершит все 370 289 287 поездок к концу ночи.
Конечно, чисто теоретически, Санта может создать даже 370 289 287 рабочих потоков, каждый из которых займется одним домом, чтобы доставить подарки всем детям! Это сделало бы Санту максимально продуктивны, а также объяснило бы, как ему удается съесть все эти печеньки с молоком, не объевшись. ????
Эффективное и счастливое многопоточное Рождество
Благодаря современным компьютерам мы наконец-то понимаем, как Санта-Клаус справляется с, казалось бы, невыполнимой задачей доставки игрушек хорошим девочкам и мальчикам по всему миру. От моей семьи вашей семье, я надеюсь, вы проводите отличное Рождество. И не за будьте повесить носки на полку маршрутизатора.
Конечно, все это никак не объясняет, как же все-таки северным оленям удается летать.
