Алгоритм – это набор четко сформулированных инструкций, который применяется для решения конкретной задачи. Эти задачи вы можете решать любым удобным для вас способом.

Шпаргалка по «О большому» – диаграмма временной сложности
Это значит, что ваш метод, который вы используете для решения задачи, может отличаться от моего, но при этом мы оба должны получить один и тот же результат.
Так как способ решения одной и той же задачи может быть не один, то должен существовать и способ оценить эти решения или алгоритмы с точки зрения оптимальности и эффективности (время, которое требуется для запуска/выполнения вашего алгоритма, и общий объем потребляемой памяти).
Этот этап довольно важный для программистов. Его цель - помочь убедиться, что их приложения работают должным образом, и помочь написать чистый программный код.
И вот здесь на первый план выходит обозначение «О большое». «О большое» - это метрика, которая определяет эффективность алгоритма. Она позволяет оценить, сколько времени занимает выполнение программного кода с различными входными данными, и измерить, насколько эффективно этот программный код масштабируется по мере увеличения размера входных данных.
Что такое «О большое»?
«О большое» показывает сложность алгоритма для наихудшего случая. Для описания сложности алгоритма здесь используются алгебраические выражения.
«О большое» определяет время выполнения алгоритма, показывая, как будет меняться оптимальность алгоритма по мере увеличения размера входных данных. Однако этот показатель не расскажет вам о том, насколько быстро работает ваш алгоритм.
«О большое» измеряет эффективность и оптимальность алгоритма, основываясь на временной и пространственной сложности.
Что такое временная и пространственная сложность?
Один из самых основных факторов, который влияет на оптимальность и эффективность вашей программы – это оборудование, ОС и ЦП, которые вы используете.
Однако при анализе оптимальности алгоритма это не учитывается. Куда важнее учесть временную и пространственную сложность как функцию, которая зависит от размера входных данных.
Временная сложность алгоритма – это то, сколько времени потребуется для выполнения алгоритма в зависимости от размера входных данных. Аналогично пространственная сложность – это то, сколько пространства или памяти потребуется для выполнения алгоритма в зависимости от размера входных данных.
В данной статье мы рассмотрим временную сложность. Эта статья станет для вас своего рода шпаргалкой, которая поможет вам понять, как можно рассчитать временную сложность для любого алгоритма.
Почему временная сложность зависит от размера входных данных?
Для того, чтобы полностью понять, что же такое «зависимость от входных данных», представьте, что у вас есть некий алгоритм, который вычисляет сумму чисел, основываясь на ваших входных данных. Если вы ввели 4, то он сложит 1+2+3+4, и на выходе получится 10; если вы ввели 5, то на выходе будет 15 (то есть алгоритм сложил 1+2+3+4+5).
const calculateSum = (input) => {
let sum = 0;
for (let i = 0; i <= input; i++) {
sum += i;
}
return sum;
};В приведенном выше фрагменте программного кода есть три оператора:
Давайте посмотрим на картинку выше. У нас есть три оператора. При этом, так как у нас есть цикл, то второй оператор будет выполняться, основываясь на размере входных данных, поэтому, если на входе алгоритм получает 4, то второй оператор будет выполняться четыре раза. А значит, в целом алгоритм выполнится шесть (4+2) раз.
Проще говоря, алгоритм будет выполняться input+2 раза; input может быть любым числом. Это говорит о том, что алгоритм выражается в терминах входных данных. Иными словами, это функция, которая зависит от размера входных данных.
Для понятия «О большое» есть шесть основных типов сложностей (временных и пространственных):
- Постоянное время: O1
- Линейное время: On
- Логарифмическое время: On log n
- Квадратичное время: On2
- Экспоненциальное время: O2n
- Факториальное время: On!
Прежде чем мы перейдем к рассмотрению всех этих временных сложностей, давайте посмотрим на диаграмму временной сложности «О большого».
Диаграмма временной сложности «О большого»
Диаграмма «О большого» - это асимптотические обозначение, которое используется для выражения сложности алгоритма или его оптимальности в зависимости от размера входных данных.
Данная диаграмма помогает программистам определить сценарий наихудшего случая, а также оценить время выполнения и объем требуемой памяти.
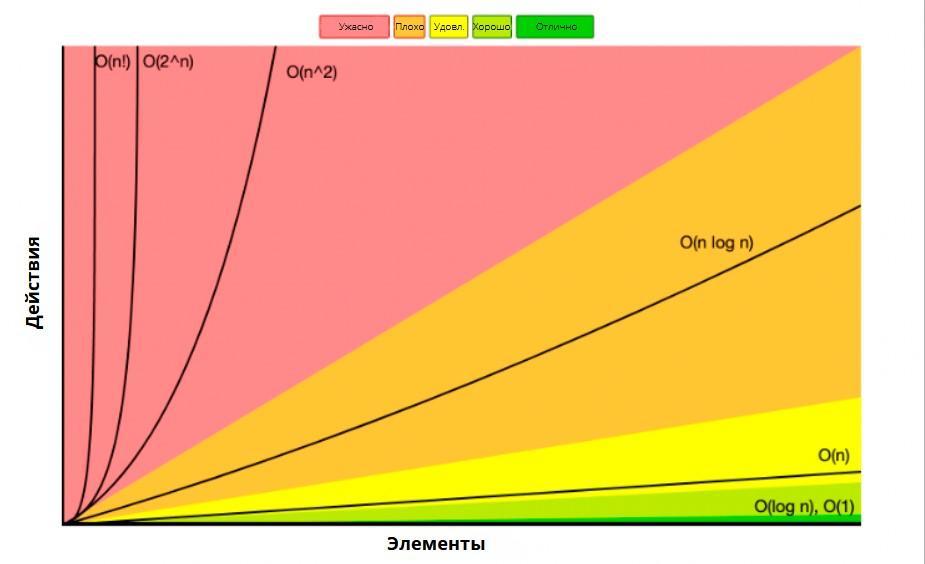
Следующий график иллюстрирует сложность «О большого»:
Глядя на приведенную выше диаграмму, можно определить, что O1 – постоянное время выполнения алгоритма, является наилучшим вариантом. Это означает, что ваш алгоритм обрабатывает только один оператор без какой-либо итерации. Дальше идет Olog n , что тоже является неплохим вариантом, и другие:
- O1 – отлично/наилучший случай
- Olog n – хорошо
- On – удовлетворительно
- On log n – плохо
- On2, O2n, On! – ужасно/наихудший случай
Теперь вы имеете представление о различных временных сложностях, а также можете понять, какие из них наилучшие, хорошие или удовлетворительные, а какие плохие и наихудшие (плохих и наихудших временных сложностей следует избегать).
Следующий вопрос, который может прийти на ум: «какой алгоритм какую сложность имеет?» И это вполне логичный вопрос, ведь эта статья задумывалась как шпаргалка. ☺
- Когда ваши расчеты не зависят от размера входных данных, то это постоянная временная сложность - O1.
- Когда размер входных данных уменьшается в два раза, например, при итерации, обработке рекурсии и т.д., то это логарифмическая временная сложность - Olog n .
- Когда у вас один цикл в алгоритме, то это линейная временная сложность - On.
- Когда у вас есть вложенные циклы, то есть цикл в цикле, то это квадратичная временная сложность - On2.
- Когда скорость роста удваивается при каждом добавлении входных данных, то это экспоненциальная временная сложность - O2n.
Давайте перейдем к описанию временных сложностей. Для каждой будут приведены примеры. Отмечу, что в примерах я использовал JavaScript, но если вы понимаете принцип и что из себя представляет каждая временная сложность, то не имеет значения, какой язык программирования вы выберите.
Примеры временных сложностей «О большого»
Постоянное время: O1
Когда алгоритм не зависит от размера входных данных n, то говорят, что он имеет постоянную временную сложность порядка O1. Это значит, что время выполнения алгоритма всегда будет одним и тем же, независимо от размера входных данных.
Допустим, что задача алгоритма – вернуть первый элемент массива. Даже если массив состоит из миллиона элементов, временная сложность будет постоянной, если использовать следующий подход для решения задачи:
const firstElement = (array) => {
return array[0];
};
let score = [12, 55, 67, 94, 22];
console.log(firstElement(score)); // 12Приведенная выше функция выполняет лишь один шаг, а это значит, что функция работает за постоянное время, и ее временная сложность O1.
Однако, как уже было сказано, разные программисты могут найти разные способы решения задачи. Например, другой программист может решить, что сначала надо пройти по массиву, а затем уже вернуть первый элемент:
const firstElement = (array) => {
for (let i = 0; i < array.length; i++) {
return array[0];
}
};
let score = [12, 55, 67, 94, 22];
console.log(firstElement(score)); // 12Это просто пример – вряд ли кто-то будет решать эту задачу таким способом. Но здесь уже есть цикл, а значит алгоритм не будет выполняться за постоянное время, здесь в игру вступает линейное время с временной сложностью On.
Линейное время: On
Линейная временная сложность возникает, когда время работы алгоритма увеличивается линейно с размером входных данных. Когда функция имеет итерацию по входному значению n, то говорят, что она имеет временную сложность порядка On.
Допустим, алгоритм должен вычислить и вернуть факториал любого числа, которое вы введете. Это значит, что если вы введете число 5, то алгоритм должен выполнить цикл и умножить 1·2·3·4·5, а затем вывести результат – 120:
const calcFactorial = (n) => {
let factorial = 1;
for (let i = 2; i <= n; i++) {
factorial = factorial * i;
}
return factorial;
};
console.log(calcFactorial(5)); // 120Тот факт, что время выполнения алгоритма зависит от размера входных данных, подразумевает наличие линейной временной сложности порядка On.
Логарифмическое время: Olog n
Это чем-то похоже на линейную временную сложность. Однако здесь время выполнения зависит не от размера входных данных, а от их половины. Когда размер входных данных уменьшается на каждой итерации или шаге, то говорят, что алгоритм имеет логарифмическую временную сложность.
Такой вариант считается вторым сверху списка лучших, так как ваша программа работает лишь с половиной входных данных. И при всем при этом, размер входных данных уменьшается с каждой итерацией.
Отличный пример – функция бинарного поиска, которая делит отсортированный массив, основываясь на искомом значения.
Допустим, что нам надо найти индекс определенного элемента в массиве с помощью алгоритма бинарного поиска:
const binarySearch = (array, target) => {
let firstIndex = 0;
let lastIndex = array.length - 1;
while (firstIndex <= lastIndex) {
let middleIndex = Math.floor((firstIndex + lastIndex) / 2);
if (array[middleIndex] === target) {
return middleIndex;
}
if (array[middleIndex] > target) {
lastIndex = middleIndex - 1;
} else {
firstIndex = middleIndex + 1;
}
}
return -1;
};
let score = [12, 22, 45, 67, 96];
console.log(binarySearch(score, 96));Приведенный выше программный код демонстрирует бинарный поиск. Судя по нему, вы сначала получаете индекс среднего элемента вашего массива, дальше вы сравниваете его с искомым значением и, если они совпадают, то вы возвращаете этот индекс. В противном случае, если они не совпали, вы должны определить, искомое значение больше или меньше среднего, чтобы можно было изменить первый и последний индекс, тем самым уменьшив размер входных данных в два раза.
Так как на каждой такой итерации размер входных данных уменьшается в два раза, то данный алгоритм имеет логарифмическую временную сложность порядка Olog n .
Квадратичное время: On2
Когда в алгоритме присутствуют вложенные циклы, то есть цикл в цикле, то временная сложность уже становится квадратичной, и здесь нет ничего хорошего.
Представьте, что у вас есть массив из n элементов. Внешний цикл будет выполняться n раз, а внутрениий – n раз для каждой итерации внешнего цикла, и, соответственно, общее количество итераций составит n2. Если в массиве было 10 элементов, то количество итераций будет 100 (102).
Ниже приведен пример, где сравниваются элементы для того, чтобы можно было вывести индекс, когда найдутся два одинаковых:
const matchElements = (array) => {
for (let i = 0; i < array.length; i++) {
for (let j = 0; j < array.length; j++) {
if (i !== j && array[i] === array[j]) {
return `Match found at ${i} and ${j}`;
}
}
}
return "No matches found 😞";
};
const fruit = ["🍓", "🍐", "🍊", "🍌", "🍍", "🍑", "🍎", "🍈", "🍊", "🍇"];
console.log(matchElements(fruit)); // "Match found at 2 and 8"В этом примере есть вложенный цикл, а значит, здесь будет квадратичная временная сложность порядка On2.
Экспоненциальное время: O2n
Экспоненциальная временная сложность появляется, когда скорость роста удваивается с каждым добавлением входных данных n, например, когда вы обходите все подмножества входных элементов. Каждый раз, когда единицу входных данных увеличивают на один, то количество итераций, которые выполняет алгоритм, увеличиваются в два раза.
Хороший пример – рекурсивная последовательность Фибоначчи. Допустим, дано число, и необходимо найти n-ый элемент последовательности Фибоначчи.
Последовательность Фибоначчи – это математическая последовательность, в которой каждое число является суммой двух предыдущих; первые два числа – 0 и 1. Третье число – 1, четвертое – 2, пятое – 3 и т.д. (0, 1, 1, 2, 3, 5, 8, 13, …).
Соответственно, если вы введете число 6, то выведется 6-й элемент в последовательности Фибоначчи – 8:
const recursiveFibonacci = (n) => {
if (n < 2) {
return n;
}
return recursiveFibonacci(n - 1) + recursiveFibonacci(n - 2);
};
console.log(recursiveFibonacci(6)); // 8Приведенный выше алгоритм задает скорость роста, которая удваивается каждый раз, когда добавляются входные данные. А значит, данный алгоритм имеет экспоненциальную временную сложность порядка O2n.
Заключение
Из данной статьи вы узнали, что такое временная сложность, как определить оптимальность алгоритма с помощью «О большого», а также рассмотрели различные временные сложности с примерами.
Получите бесплатные уроки на наших курсах
- Этичный хакинг
- MongoDB для разработчиков и DevOps
- полный курс по Git
- DevOps с нуля
- Аналитик данных с нуля