Корпоративные сети →Теория→Основы сетей

Сети | Одноадресные пути без петель

Освобождаемся от петель

Декабрь 27, 2020 Мерион Нетворкс

6 минут чтения

Перед тем как начать: почитайте про перераспределение между плоскостями управления в сетях.

Обучайся в Merion Academy

Пройди курс по
сетевым технологиям

Начать

Сетевые инженеры обычно думают, что плоскость управления выполняет самые разные задачи, от вычисления кратчайшего пути через сеть до распределения политики, используемой для пересылки пакетов. Однако идея кратчайшего пути проникает в концепцию оптимального пути. Точно так же идея политики также проникает в концепцию оптимизации сетевых ресурсов. Хотя важны и политика, и кратчайший путь, ни один из них не лежит в основе того, что делает плоскость управления. Задача плоскости управления - сначала найти набор путей без петель через сеть. Оптимизация - хорошее дополнение, но оптимизация может быть "сделана" только в контексте поиска набора путей без петель.

Таким образом, в этом разделе будет дан ответ на вопрос: как плоскость управления вычисляет пути без петель через сеть?

Этот цикл статей начнется с изучения взаимосвязи между кратчайшим или наименьшим метрическим путем и безцикловыми путями. Следующая рассматриваемая тема - свободные от циклов альтернативные пути (LFA), которые не являются лучшими путями, но все же свободны от циклов. Такие пути полезны при проектировании плоскостей управления, которые быстро переключаются с наилучшего пути на альтернативный путь без петель в случае сбоев или изменений в топологии сети. Затем обсуждаются два конкретных механизма, используемых для поиска набора безцикловых путей.

Какой путь свободен от петель?

Связь между кратчайшим путем, обычно в терминах метрик, и свободными от циклов путями довольно проста: кратчайший путь всегда свободен от циклов. Причина этой связи может быть выражена наиболее просто в терминах геометрии (или, более конкретно, теории графов, которая является специализированной областью изучения в рамках дискретной математики). Рисунок 1 используется для объяснения этого.

Какие есть пути из A, B, C и D к месту назначения?

• Из A: [B, H]; [C, E, H]; [D, F, G, H]
• Из B: [H]; [A, C, E, H]; [A, D, F, G, H]
• Из D: [F, G, H]; [A, C, E, H]; [A, B, H]

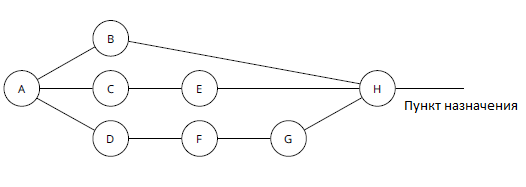
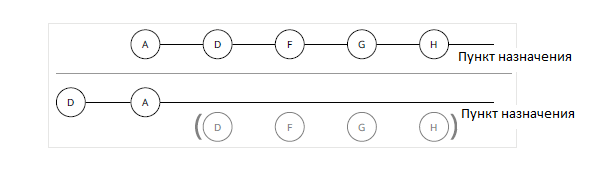
Если каждое устройство в сети должно выбирать путь, который оно будет использовать к месту назначения независимо (без привязки на путь, выбранный любым другим устройством), можно сформировать постоянные петли. Например, A может выбрать путь [D, F, G, H], а D может выбрать путь [A, C, E, H]. Затем устройство A будет перенаправлять трафик к пункту назначения в D, а D затем перенаправит трафик к пункту назначения в A. Должно быть какое-то правило, отличное от выбора пути, реализованного алгоритмом, используемым для вычисления пути на каждом устройстве, например, выбрать самый короткий (или самый дешевый) путь. Но почему выбор кратчайшего (или самого дешевого) пути предотвращает возникновение петли? Рисунок 2 иллюстрирует это.

На рисунке 2 предполагается, что A выбирает путь [D, F, G, H] к месту назначения, а D выбирает путь через A к месту назначения. Чего D не может знать, поскольку он вычисляет путь к месту назначения, не зная, что вычислил A, так это того, что A использует путь через D сам для достижения места назначения. Как может плоскость управления избежать такого цикла? Обратите внимание на то, что стоимость пути вдоль цикла всегда должна включать стоимость цикла, а также элемент пути без петель. В этом случае путь через A с точки зрения D должен включать стоимость от D до места назначения. Следовательно, стоимость через A, с точки зрения D, всегда будет больше, чем наименьшая доступная стоимость из D. Это приводит к следующему наблюдению:

Путь с наименьшей стоимостью (или кратчайший) не может содержать путь, который проходит через вычислительный узел или, скорее, кратчайший путь всегда свободен от петель.

В этом наблюдении есть два важных момента.

Во-первых, это наблюдение не говорит о том, что пути с более высокой стоимостью являются определенно петлями, а только о том, что путь с наименьшей стоимостью не должен быть петлей. Можно расширить правило, чтобы обнаружить более широкий набор путей без петель, помимо пути с наименьшей стоимостью- они называются альтернативами без петель (Loop-Free Alternates).

Во-вторых, это наблюдение справедливо, только если каждый узел в сети имеет одинаковое представление о топологии сети. Узлы могут иметь разные представления о топологии сети по ряду причин, например:

• Топология сети изменилась, и все узлы еще не были уведомлены об изменении; отсюда и микропетли.
• Некоторая информация о топологии сети была удалена из базы данных топологии путем суммирования или агрегирования.
• Метрики настроены так, что путь с наименьшей стоимостью несовместим с разных точек зрения.

Плоскости управления, используемые в реальных сетях, тщательно продуманы, чтобы либо обойти, либо минимизировать влияние различных устройств, имеющих разные представления о топологии сети, что потенциально может привести к зацикливанию пути. Например:

• Плоскости управления тщательно настраиваются, чтобы минимизировать разницу во времени между изучением изменения топологии и изменением пересылки (или отбрасывать трафик во время изменений топологии, а не пересылать его).
• При обобщении топологии или агрегировании достижимости необходимо позаботиться о сохранении информации о затратах.
• "Лучшие общепринятые практики" проектирования сети поощряют использование симметричных метрик, а многие реализации затрудняют или делают невозможным настройку каналов с действительно опасными показателями, такими как нулевая стоимость канала.

Часто требуется много работы, чтобы найти, обойти или предотвратить непреднамеренное нарушение правила кратчайшего пути в реальных протоколах плоскости управления.

Почему бы не использовать список узлов?

На этом этапе должен возникнуть очевидный вопрос: почему бы просто не использовать список узлов для поиска маршрутов без петель? Например, на рисунке 1, если A вычисляет путь через D, может ли D каким-то образом получить путь, вычисленный A, обнаружить, что сам D находится на пути, и, следовательно, не использовать путь через A?

Первая проблема с этим механизмом заключается в процессе обнаружения. Как D должен узнать о пути, выбранном A, и A узнать о пути, выбранном D, не вызывая состояния гонки? Два устройства могут выбрать друг друга в качестве следующего перехода к пункту назначения в один и тот же момент, а затем информировать друг друга в один и тот же момент, в результате чего оба одновременно выбирают другой путь. Результатом может быть либо стабильный набор путей без петель, когда два устройства циклически выбирают друг друга и не имеют пути к месту назначения, либо состояние насыщения, при котором нет пути к месту назначения.

Вторая проблема с этим механизмом - резюмирование - преднамеренное удаление информации о топологии сети для уменьшения количества состояний, переносимых на уровне управления. Плоскость управления будет иметь только метрики, с которыми можно работать, везде, где обобщается топология. Следовательно, лучше использовать правило, основанное на метриках или стоимости, а не на наборе узлов, через которые проходит путь.

Обратите внимание, что обе эти проблемы решаемы. На самом деле существуют алгоритмы вектора пути, которые полагаются на список узлов для вычисления путей без петель через сеть. Хотя эти системы широко распространены, они часто считаются слишком сложными для развертывания во многих ситуациях, связанных с проектированием сетей. Следовательно, широко используются системы на основе метрик или стоимости.

Теперь почитайте материал про построение деревьев в сетях